printf("ho_tari\n");
ep.41 신경망학습, 오차역전파법 본문
2024.9.3
신경망 학습
데이터에서 학습한다.
학습 (지도학습을 사용함)
- 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것
손실함수 (오차를 구함)
- 신경망이 학습할 수 있도록 해주는 지표
학습의 목표 - 오차가 가장 적게하는 매개 변수의 값을 찾는 것
- 손실 함수의 결과값을 가장 작게 만드는 가중치 매개 변수 값을 찾는 것
경사강하법
- 손실 함수의 값을 가급적 작게 만드는 기법
- 함수의 기울기를 활용 - 오차에 대한 미분을 구하고 매개변수에서 오차를 줄이는 방향으로 연산한다.
데이터 주도 학습
- 기계학습은 데이터가 생명이다. (데이터는 경험이라 볼수 있다.)
- 데이터에서 답을 찾고 데이터에서 패턴을 발견하고 데이터로 이야기를 만드는 것
손글씨 숫자 '5'의 예 : 사람마다 자신만의 필체가 있다.

사람'손으로 규칙만들기에서 '기계'가 데이터로 부터 배우는 방식으로의 패러다임 전환 : 회색 블록은 사람이 개입하지 않음을 뜻한다.

훈련데이터와 시험 데이터
- 훈련데이터를 사용하여 학습하면서 최적의 매개변수를 찾는다.
- 시험 데이터를 사용하여 앞서 훈련한 모델의 실력을 평가한다.
- 범용 능력을 제대로 평가하기 위해 훈련데이터와 시험데이터를 분리
- 범용 능력이란 아직 보지 못한 즉 훈련 데이터에 포함되지 않은 데이터로 문제를 올바르게 풀어내는 능력
- 데이터셋 하나로만 매개변수의 학습과 평가를 수행하면 올바른 평가가 될 수 없다.
- 수중의 데이터셋은 제대로 맞히더라도 다른 데이터셋에는 엉망인 일도 벌어진다.
- 한 데이터셋에만 지나치게 최적화된 상태를 오버피팅이라 한다.
손실 함수
- 오차를 구함
- loss function / cost function / object fucntion
- 신경망 학습에서 사용하는 지표 - 학습이 잘 진행되고 있는지 판단
- 평균 제곱 오차(선형)와 교차 엔트로피(비선형) 오차 사용
평균 제곱 오차
- Mean Square Error
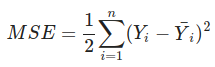
import numpy as np
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # one hot encoding에 대한 개념 이해 필요
y = [0.05, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
# 4.2.1 평균 제곱 오차
# E = 1/2 * ∑ _k (yk-tk)²
# yk : 신경망의 출력
# tk : 정답 레이블
# k : 데이터의 차원 수
mse = mean_squared_error(np.array(y), np.array(t))
print(mse) # 0.09375교차 엔트로피 오차
- Corss Entropy Error

- 여기에서 log는 밑이 e인 자연로그
- y는 신경망의 출력, t는 정답 레이블
- 정답레이블은 정답에 해당하는 인덱스의 값만 1이고 나머지는 0

자연로그 y=logx의 그래프
%matplotlib inline
import matplotlib.pylab as plt
x = np.arange(0.001, 1.0, 0.001)
y = np.log(x)
plt.plot(x, y)
plt.ylim(-5.0, 0.0) # y축의 범위 지정
plt.show()x가 1일 때 y는 0이 되고 x가 0에 가까워질 수록 y의 값은 점점 작아짐
- 교차 엔트로피 구현
def cross_entropy_error(y, t):
delta = 1e-7 # 0일때 -무한대가 되지 않기 위해 작은 값을 더함
return -np.sum(t * np.log(y + delta))
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 정답 1 오답 0
y_1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# 3번째 값만 cross entropy
cee = cross_entropy_error(np.array(y_1), np.array(t))
print("handmade :",end=' ')
# 정답일때의 y값만 반영한 결과
print(-np.log(0.1))
print("using_cee:",end= ' ')
print(cee) # 0.510825457099
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cee = cross_entropy_error(np.array(y), np.array(t))
print(cee) # 2.30258409299미니배치 학습
- 지금까지는 데이터 하나에 대한 손실함수를 고려함
- 훈련데이터 모두에 대한 손실함수의 합을 구해야 함
- 평균 손실함수를 구함
- 일부를 추려 전체의 근사치로 이용
- 훈련데이터로 부터 일부만 골라 학습 수행
Mni batch

- MNIST 데이터셋은 훈련데이터 60,000개
- 모든 데이터를 대상으로 손실함수의 합을 구하려면 시간이 걸림
- 빅데이터 수준이면 전체 손실함수의 합을 구하면 시간이 상당히 걸림
- 이 많은 데이터를 대상으로 일일이 손실 함수를 계산하는 것은 현실적이지 않다.
- 데이터 일부를 추려 전체의 근사치로 이용
- 이를 미니배치라 한다.
- 60,000장의 훈련 데이터 중에서 100장을 무작위로 뽑아 그 100장을 학습하는 것을 말한다. 이러한 학습 방법을 미니배치 학습이라고 한다.
무작위로 골라내는 코드 작성
- MNIST를 다운로드 받아서 10개의 데이터를 무작위로 선택하는 코드
- MNIST 다운로드
import tensorflow as tf
(x_train, t_train), (x_test, t_test) = tf.keras.datasets.mnist.load_data()
t_train=tf.keras.utils.to_categorical(t_train)
x_train=x_train.reshape(60000,-1)
print(x_train.shape)
print(t_train.shape)10개의 데이터 셋 추출
train_size = x_train.shape[0] #
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
print(x_batch)
print(t_batch)
for i in range(10):
img = x_batch[i].reshape(28,28)
plt.imshow(img, cmap='gray')
plt.show()
np.random.choice(60000, 10) # 60000개 중에 10개 무작위 선택
(배치용)교차 엔트로피 오차 구현하기
- 배치의 크기로 나누어 오차를 구한다.(batch_size)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y)) / batch_size ##### 이부분을 수정함
def cross_entropy_error(y, t):
if y.ndim == 1: # batch가 1인 경우는 1차원으로 결과가 나온다.
t = t.reshape(1, t.size) # 2차원으로 변경
y = y.reshape(1, y.size) # 2차원으로 변경
#정답 t가 2차원으로 되어져 있어서 차원을 맞추어야 합니다.
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
#if t.size == y.size:
# t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size- 정답에 해당하는 값이 1이고 나머지는 0 이므로 정답에 해당하는 값만 구하면 된다.
- batch_size = 5
- np.arange(batch_size)는 [0, 1, 2, 3, 4] 넘파이 배열 생성
- t에는 레이블 [2, 7, 0, 9, 4]
- y[np.arange(batch_size),t]는 [y[0,2], y[1,7], y[2,0], y[3,9], y[4,4]]
왜 손실 함수를 설정하는가?
- 정확도와 오차 중에 오차를 기준으로 매개변수를 값을 변화시킨다.
- 정확도는 매개변수의 미소한 변화에는 반응을 보이지 않고, 반응이 있더라도 그 값이 불연속적으로 갑자기 변화한다.
- 신경망 학습에서는 최적의 매개변수(가중치 w와 편향 b)를 탐색할 때 손실 함수 값을 가능한 작게하는 매개변수를 찾는다.
- 오차에 대한 매개변수의 미분(정확히는 기울기)을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정 반복
- 미분 값이 음수이면 그 가중치 매개변수를 양의 방향으로 약간 감소
- 미분 값이 양수이면 그 가중치 매개변수를 음의 방향으로 약간 증가
- 미분값이 0이면 증가도 감소도 하지 않고 유지됨
계단 함수와 시그모이드 함수 : 계단 함수는 대부분의 위치에서 기울기가 0이지만, 시그모이드 함수의 기울기(접선)는 0이 아니다.

- 계단함수의 미분은 O인곳을 제외하고 0이다. 그러므로 손실함수(오차)를 지표로 삼는 것에 아무런 의미가 없다.
- 시그모이드 함수의 미분은 어느 장소라도 0이 되지 않는다.
- 이는 신경망 학습에서 중요한 성질로, 기울기가 O이 되지 않는 덕분에 신경망이 올바르게 학습할 수 있는 것이다.
수치 미분
- 경사법에서는 기울기(경사) 값을 기준으로 나아갈 방향을 정한다.
- 기울기를 알아내는 미분에 대하여 복습한다.
미분
- 미분은 한순간의 변화량을 표시한다.
- 한순간은 시간의 간격이 아주 적은 시간의 차이를 의미
수치 미분
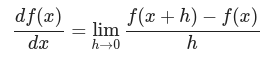
- 좌변은 f(x)의 x에 대한 미분을 나타내는 기호
- x의 작은 변화가 함수 f(x)를 어떻게 변화시키느냐를 의미함
- 이 때 시간의 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미
- 반올림 오차를 주의해야 하며 진정한 미분이 아니므로 중심차분으로 계산해야하는 것에 주의해야 한다.
#나쁜 구현 예
def numerical_diff(f, x):
h = 10e-50
return (f(x + h) - f(x)) / (h)- 너무 작은 h 값은 반올림 오차를 유발 시킨다.
- 반올림 오차는 작은 값이 생략되어 최종 계산 결과에 오차가 발생한다.
np.float32(1e-50)- 반올리 오차가 발생하므로 1e-4 정도가 적당하다.
진정한 미분(진정한 접선)과 수치 미분(근사로 구한 접선)의 값은 다르다.
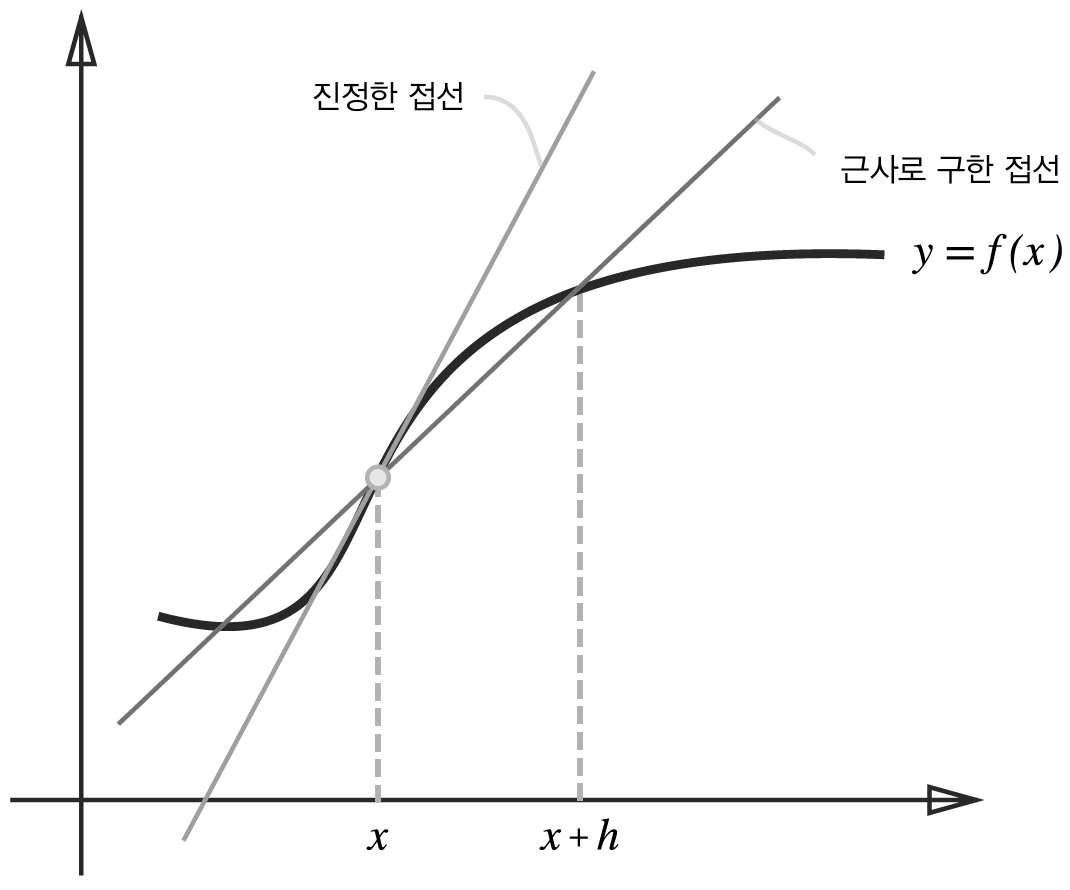

- 프로그램으로는 h를 무한히 좁이는 것이 불가능하다.
- h 사이에서 변화가 있으면 기울기 값의 왜곡이 발생한다.
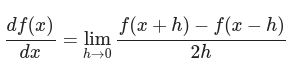

- 수치 미분에서 오차를 줄이기 위해 (x + h)와 (x - h) 일 때의 함수 f의 차분을 계산하는 방법을 쓰기도 한다.
- 이 차분은 x를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분 또는 중앙 차분이라 한다.
접점에서의 기울기 구하는 코드

import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
# 접점에서의 기울기
# 미분값
def function_1(x):
return 0.01*x**2 + 0.1*x
#0.01 x2 + 0.1x
def tangent_line(f, x):
d = numerical_diff(f, x)
y = f(x) - d*x
return lambda t: d*t + y #아래와 같음
#return d*t + y
x = np.arange(-30.0, 20.0, 0.1)
y = function_1(x)
# first
plt.figure(figsize=(16, 16))
tf = tangent_line(function_1, 5)
y2 = tf(x)
plt.subplot(221)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.ylim(-1,6)
plt.plot(x, y)
plt.plot(x[300:400],y2[300:400])
plt.scatter(5,function_1(5),c='r')
# second
tf_2=tangent_line(function_1, 10)
y3=tf_2(x)
plt.subplot(222)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.ylim(-1,6)
plt.scatter(10,function_1(10),c='r')
plt.plot(x, y)
plt.plot(x[350:450],y3[350:450])
#third
tf_2=tangent_line(function_1, 1)
y3=tf_2(x)
plt.subplot(223)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.ylim(-1,6)
plt.scatter(1,function_1(1),c='r')
plt.plot(x, y)
plt.plot(x[250:350],y3[250:350])
#forth
#plt.figure(figsize=(16, 16))
tf_2=tangent_line(function_1, -5)
y4=tf_2(x)
plt.subplot(224)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.ylim(-1,6)
plt.scatter(-5,function_1(-5),c='r')
plt.plot(x, y)
plt.plot(x[200:300],y4[200:300])
plt.show()
편미분
- 변수가 두개라는 것에 주의
- 그래프를 그리면 3차원으로 그려진다.

def function_2(x):
return x[0]**2 + x[1]**2
# 또는 return sum(x**2)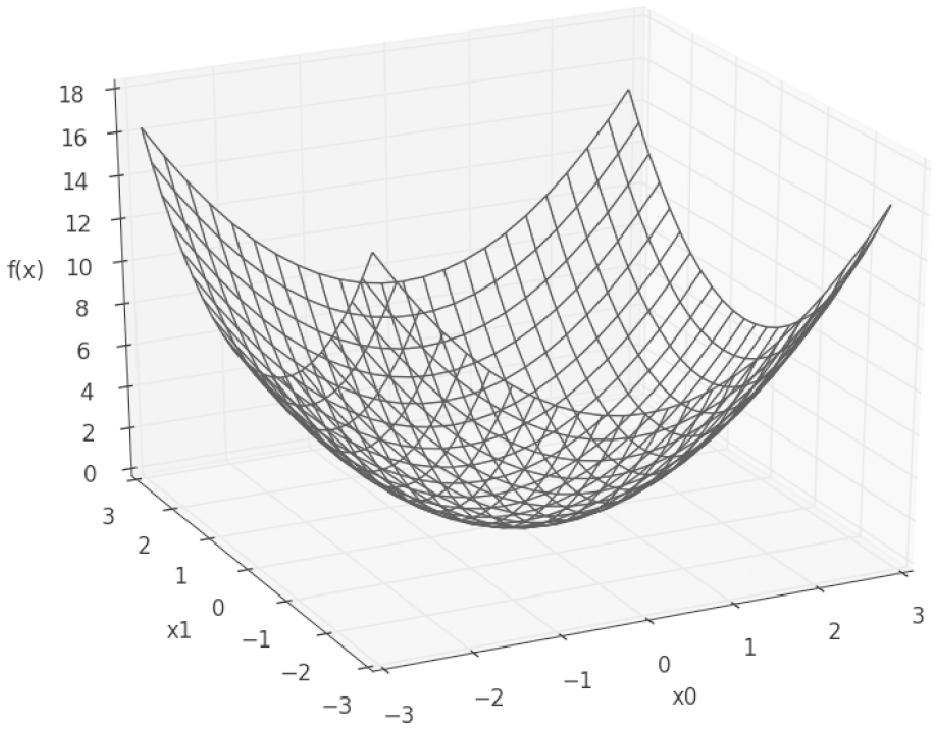
- 어느 변수에 대한 미분이냐, 즉 x0와 x1 중 어느 변수에 대한 미분이냐를 구분해야 한다.
- 변수가 여러개인 함수에 대한 미분을 편미분이라고 한다.
- 수식으로 아래와 같다.
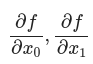
- 여러개의 변수에서 한개를 변수로 선택하고 나머지를 상수처럼 처리해서 미분값을 구한다.
기울기
def numerical_gradient(f, x):
#점에서의 기울기 계산
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
#print("fx1:")
#print(fxh1,fxh2)
grad[idx] = (fxh1 - fxh2) / (2 * h)
#print(grad[idx])
x[idx] = tmp_val # 값 복원
return grad
def function_2(x):
return x[0]**2 + x[1]**2
# or return np.sum(x**2)
# 이 아래에서 print 값은 x[0] 편미분 값 x[1] 편미분값
print(numerical_gradient(function_2, np.array([3.0, 4.0]))) # [ 6. 8.]
print(numerical_gradient(function_2, np.array([0.0, 2.0]))) # [ 0. 4.]
print(numerical_gradient(function_2, np.array([3.0, 0.0]))) # [ 6. 0.]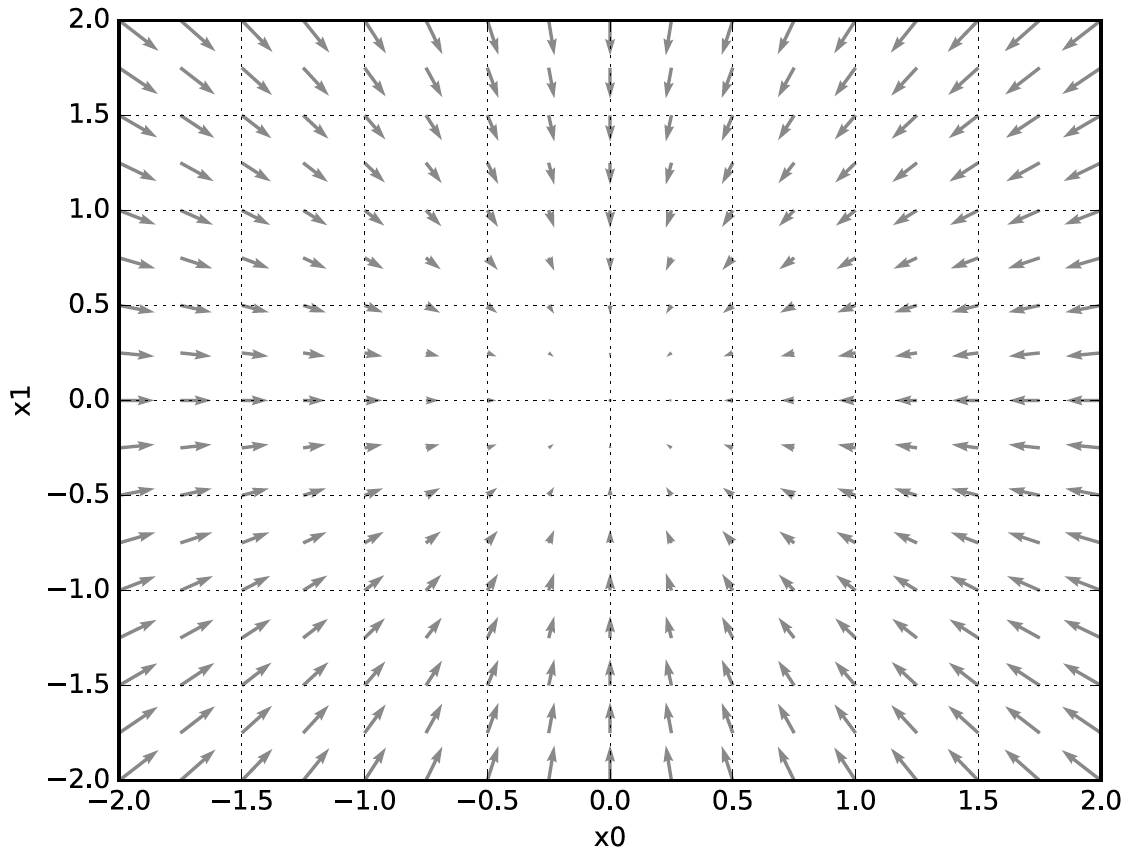
- 기울기 그림은 방향을 가진 벡터(화살표)로 그려집니다.
- 기울기가 가장낮은 장소를 가르킨다.
- 기울기가 가르키는 쪽은 각 장소에서 함수의 출력 값을 가장 줄이는 방향
경사법(경사 하강법)

갱신과정 : 점선은 함수의 고등선을 나타낸다.

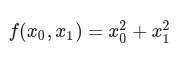
의 최소값
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
# 경사법으로 f(x0, x1) = x0² + x1²의 최솟값을 구해라
init_x = np.array([-3.0, 4.0])
x, x_history = gradient_descent(function_2, init_x, lr=0.1)
print(x) # [ -6.11110793e-10 8.14814391e-10]
# 학습률이 너무 큼
init_x = np.array([-3.0, 4.0])
x, x_history = gradient_descent(function_2, init_x, lr=10.0)
print(x) # [ -2.58983747e+13 -1.29524862e+12] 발산함
# 학습률이 너무 작음
init_x = np.array([-3.0, 4.0])
x, x_history = gradient_descent(function_2, init_x, lr=1e-10)
print(x) # [-2.99999994 3.99999992] 거의 변화 없음
# 그래프
init_x = np.array([-3.0, 4.0])
x, x_history = gradient_descent(function_2, init_x, lr=0.1, step_num=100)
plt.figure(figsize=(16, 16))
plt.subplot(222)
plt.plot([-5, 5], [0, 0], '--b')
plt.plot([0, 0], [-5, 5], '--b')
plt.plot(x_history[:, 0], x_history[:, 1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.figure(figsize=(16, 16))
plt.subplot(223)
init_x = np.array([-3.0, 4.0])
#x, x_history = gradient_descent(function_2, init_x, lr=0.0001, step_num=100)
#x, x_history = gradient_descent(function_2, init_x, lr=0.001, step_num=100)
x, x_history = gradient_descent(function_2, init_x, lr=0.005, step_num=100)
plt.plot([-5, 5], [0, 0], '--b')
plt.plot([0, 0], [-5, 5], '--b')
plt.plot(x_history[:, 0], x_history[:, 1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()- simplet net
- softmax 는 확률값
- loss 는 계산한 값과 확률 값을 리턴

신경망에서 기울기
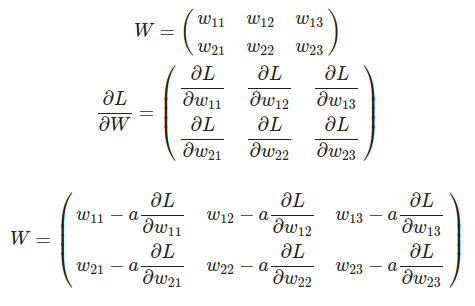
SimpleNet과 TwoLayerNet를 위한 함수 구현
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 수치미분 함수에서는 반복문 for 문을 사용하지 않고 np.nditer 를 사용하여 반복문을 처리하는 구문을 사용하였습니다.
# numerical_gradient 함수의 인자 f는 Loss 함수 이고 인자 x는 weight 값인데 2차원으로 되어져 있어서 단순히 for 문을 사용을 할 수 없습니다.
# 이러한 경우 np.nditer를 사용하여 반복문을 작성해야 합니다.
# 참고 사이트 입니다.
# https://kosb.tistory.com/42
# https://numpy.org/doc/stable/reference/generated/numpy.nditer.html
# https://transferhwang.tistory.com/278
# https://homzzang.com/b/py-318
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) # 1
while not it.finished: # 2
idx = it.multi_index # 3
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 값 복원
it.iternext() # 4
return gradSimple Network class 구현
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3) # 정규분포로 초기화
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
net = simpleNet()
print(net.W)
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
z=net.predict(x)
y = softmax(z)
print(y)
for i in range(10000):
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
print(net.loss(x, t))
#print(f(w)))
net.W -= 0.001 * dW
#print(net.W)
z=net.predict(x)
y = softmax(z)
print(y)
학습 알고리즘 구현하기
- 1단계 미니 배치
- 2단계 기울기 산출
- 3단계 매개변수 갱신
- 4단계 반복
2층 신경망 클래스 구현하기
Two Layer Network class 구현
class TwoLayerNet:
"""
params : 신경망의 매개변수를 보관하는 딕셔너리 변수.
params['W1']은 1번째 층의 가중치, params['b1']은 1번째 층의 편향.
params['W2']은 2번째 층의 가중치, params['b2']은 2번째 층의 편향.
grad : 기울기를 보관하는 딕셔너리 변수(numerical_gradient()의 반환값)
grads['W1']은 1번째 층의 가중치의 기울기, grads['b1']은 1번째 층의 편향의 기울기.
grads['W2']은 2번째 층의 가중치의 기울기, grads['b2']은 2번째 층의 편향의 기울기.
"""
# 초기화를 수행한다.
def __init__(self, input_size, hidden_size, output_size,
weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * \ #
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 예측(추론)을 수행한다.
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
#sigmoid 활성화함수
# softmax y의 확률값
return y
# 손실 함수의 값을 구한다.
# x : 입력데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
#결과의 확률값과 원핫인코딩된 값을 비교
return cross_entropy_error(y, t)
# 정확도를 구한다.
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 가중치 매개변수의 기울기를 구한다.
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
''' '''
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
#print(x.shape)
#print(W1.shape)
#print(b1.shape)
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
print(net.params['W1'].shape) # (784, 100)
print(net.params['b1'].shape) # (100,)
print(net.params['W2'].shape) # (100, 10)
print(net.params['b2'].shape) # (10,)
x = np.random.rand(100, 784) # 더미 입력 데이터(100장 분량)
y = net.predict(x)
print(y.shape)수치 미분으로 gradient descent 구현하기
- 실행하는데 시간이 많이 걸림
- 수치 미분이 너무 많은 시간이 걸리는 것을 보여주는 예제 임으로 실행되는 중간에 중단시켜도 무방함
x = np.random.rand(100, 784) # 더미 입력 데이터(100장 분량)
t = np.random.rand(100, 10) # 더미 정답 레이블(100장 분량)
grads = net.numerical_gradient(x, t) # 기울기 계산
# 주의 : 실행하는데 아주 오래걸림
# 나중에 표시 필요
print(grads['W1'].shape) # (784, 100)
print(grads['b1'].shape) # (100,)
print(grads['W2'].shape) # (100, 10)
print(grads['b2'].shape) # (10,)
미니배치 학습 구현하기
- 학습만 진행됨
- test는4.5.3에서 진행
- 미니배치 : 훈련 데이터 중 일부를 무작위로 꺼내고(미니배치), 그 미니배치에 대하여 경사법으로 매개변수를 갱신한다.
손실함수의 추이 : 왼쪽은 10,000회 반복까지의 추이, 오른쪽은 1000회 반복까지의 추이
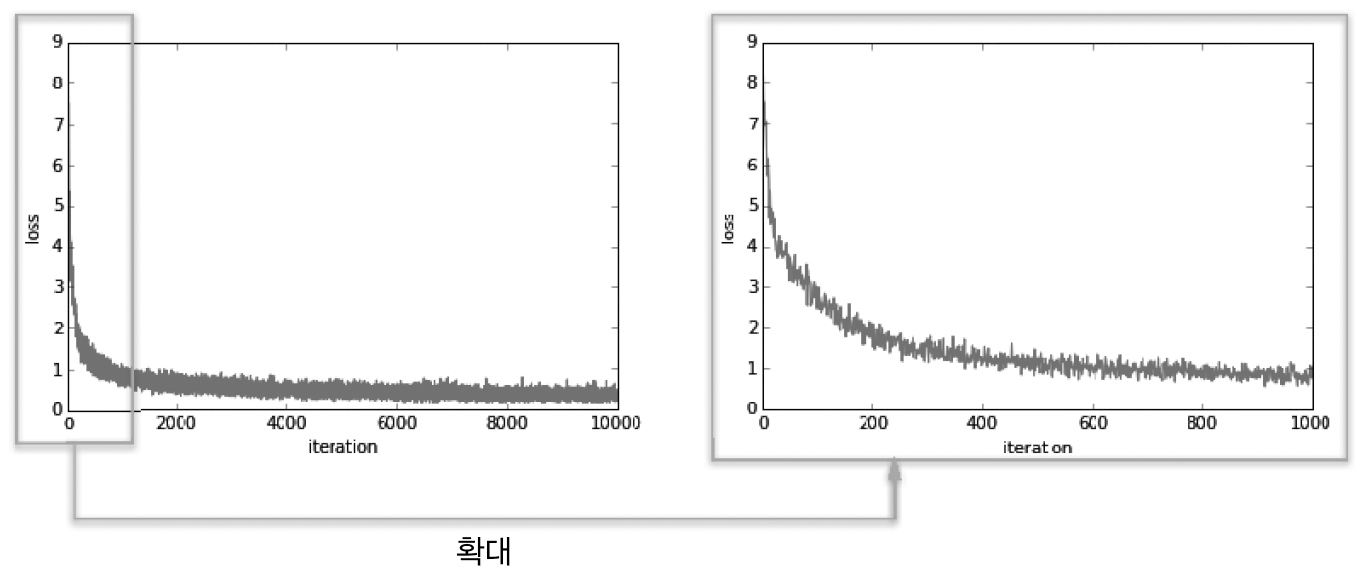
수치 미분과 공식에 의한 미분의 차이를 보기 위해서 아래와 같이 두번 실행한다.
- grad = network.numerical_gradient(x_batch, t_batch)
- #grad = network.gradient(x_batch, t_batch)
한번씩 주석을 풀고 실행해 보면 실행 속도를 알 수 있을 것이다.
import tensorflow as tf
(x_train, t_train), (x_test, t_test) = tf.keras.datasets.mnist.load_data()
t_train=tf.keras.utils.to_categorical(t_train)
t_test=tf.keras.utils.to_categorical(t_test)
x_train=x_train.reshape(60000,-1)
x_test=x_test.reshape(10000,-1)
train_loss_list = []
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 그래프 그리기
x = np.arange(len(train_loss_list))
plt.plot(x, train_loss_list, label='train loss')
plt.xlabel("epochs")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend() # 위
#plt.legend(loc='lower right') # 아래
plt.show()시험 데이터로 평가하기
import tensorflow as tf
(x_train, t_train), (x_test, t_test) = tf.keras.datasets.mnist.load_data()
t_train=tf.keras.utils.to_categorical(t_train)
t_test=tf.keras.utils.to_categorical(t_test)
x_train=x_train.reshape(60000,-1)
x_test=x_test.reshape(10000,-1)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1에폭당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
print("\n\n\n훈련데이터와 시험 데이터에 대한 정확도 추이")
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show() #acc 값 보여주기
정리
- 손실함수(지표)를 기준으로 그 값이 가장 작아지는 가중치 매개변수 값을 찾아내는 것이 신경망 학습의 목표
- 배운것
- 기계학습에서 사용하는 데이터셋은 훈련 데이터와 시험데이터로 나눠 사용한다.
- 훈련 데이터에서 학습한 모델의 범용 능력을 시험 데이터로 평가한다.
- 신경망 학습은 손실 함수를 지표로, 손실 함수의 값이 작아지는 방향으로 가중치 매개변수를 갱신한다.
- 가중치 매개변수를 갱신할 때는 가중치 매개변수의 기울기를 이용하고, 기울어진 방향으로 가중치의 값을 갱신하는 작업을 반복한다.
- 아주 작은 값을 주었을 때의 차분으로 미분을 구하는 것을 수치 미분이라고 한다.
- 수치 미분을 이용해 가중치 매개변수의 기울기를 구할 수 있다.
- 수치 미분을 이용한 계산에는 시간이 걸리지만, 그 구현은 간단하다. 한편, 다음 장에서 구현하는 다소 복잡한 오차역전파법은 기울기를 고속으로 구할 수 있다.
Back Propagation.
역전파의 계산 방법은 신호에 해당 레이어의 편미분 값을 곱하여 다음 노드로 전달하는 방법으로 계산한다.


gradient descent

오차 역전법
- 신경망의 가중치 매개변수의 오차에 대한 기울기(가중치 매개변수에 대한 손실함수의 기울기)
- 수치 미분 : 단순하고 구현하기 쉽지만 계산시간이 오래 걸린다.
- 오차역전파법 backpropagation
오차 역전법의 이해
- 수식이해 또는 computational garaph로 이해
- 시각적인 이해
계산 그래프
- 계산 과정을 노드와 화살표로 표현
- 노드 : 원으로 표시 원안에 연산내용을 적는다.
- 계산 결과를 화살표에 적음
- 왼쪽에서 오른쪽으로 전개됨
- 국소적 계산, 중간 계산 결과를 모두 보관, 역전파를 통한 미분을 효율적으로 계산
계산그래프를 통한 문제 풀이
- 계산 그래프를 구성한다.
- 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.
문제 1 : 현빈군은 1개에 100원인 사과 2개를 샀습니다. 이때 지불 금액을 구하세요. 단, 소비세가 10% 부과됩니다.
계산 그래프로 풀어본 문제 1의 답(2와 1.1을 연산으로 취급)

사과의 갯수와 소비세를 변수로 취급해 원 밖에 표시

문제 2 : 현빈군은 슈퍼에서 사과를 2개, 귤을 3개 샀습니다. 사과는 1개에 100원, 귤은 1개 150원입니다. 소비세가 10%일 때 지불 금액을 구하세요.
계산 그래프로 풀어본 문제 2의 답(덧셈 새로이 등장)

국소적 계산
- 계산 그래프의 특징은 국소적 계산을 전파함으로써 최종 결과를 얻는 다는 점
- 국소적이란 자신과 직접 관계된 작은 범위
- 자신과 관계된 계산외에는 아무것도 신경 쓸 것이 없다
사과 2개를 포함해 여러 식품을 구입하는 예

계산 그래프로 푸는 이유
- 국소적 계산
- 중간 계산 결과를 모두 보관
- 역전파를 통한 미분을 효율적으로 계산
역전파에 의한 미분값의 전달
- 미분값은 사과 값이 아주 조금 올랐을 때 지불 금액이 얼마나 올랐는가를 표시
- 사과 가격에 대한 지불 금액의 미분 값은 2.2
- 사과가 1원 오르면 최종금액은 2.2원 오른다는 뜻
- 사과 갯수와 소비세의 미분도 같은 원리로 구한다
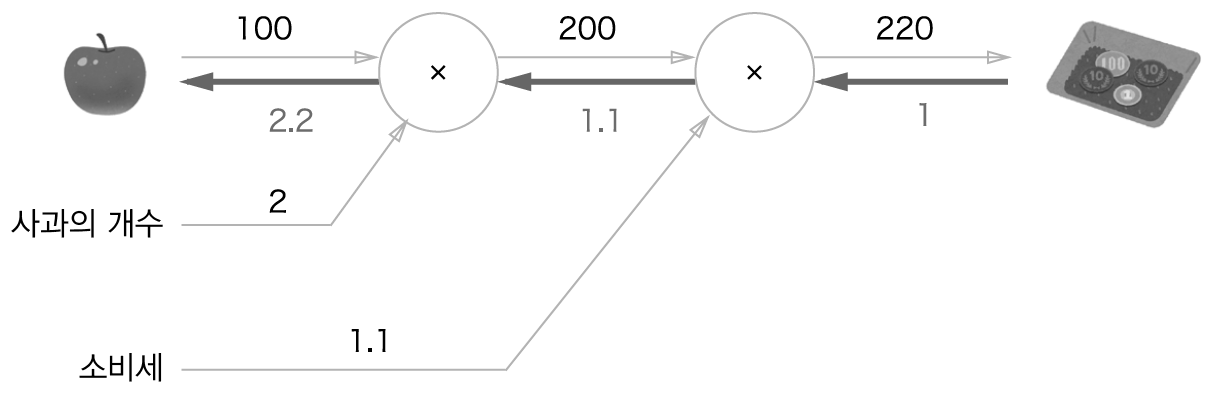
- 미분 값은 사과 값이 아주 조금 올랐을 때 지불 금액이 얼마나 증가했는가 표시
- 사과 가격에 대한 지불 금액의 미분 - 계산 그래프의 역전파로 구함
- 사과 가격에 대한 지불 금액의 미분 값은 2.2
- 사과가 1원 오르면 최종 금액은 2.2원 오른다는 뜻
- 분업해서 따로 따로 구하여 필요할 때 사용 - 효율적
연쇄 법칙
- 합성 함수(여러함수로 구성된 함수)의 미분에 대한 성질
- 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다
computational graph의 역전파 : 순방향과는 반대방향으로 국소적 미분을 곱한다
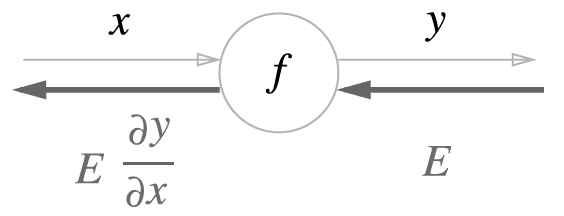
- E 상류에서 전달된 값
- 국소적으로 계산 후 상류에서 전달된 값을 곱함
합성 함수

연쇄법칙

computational graph : 순전파와는 반대 방향으로 국소적 미분을 곱하여 전달한다
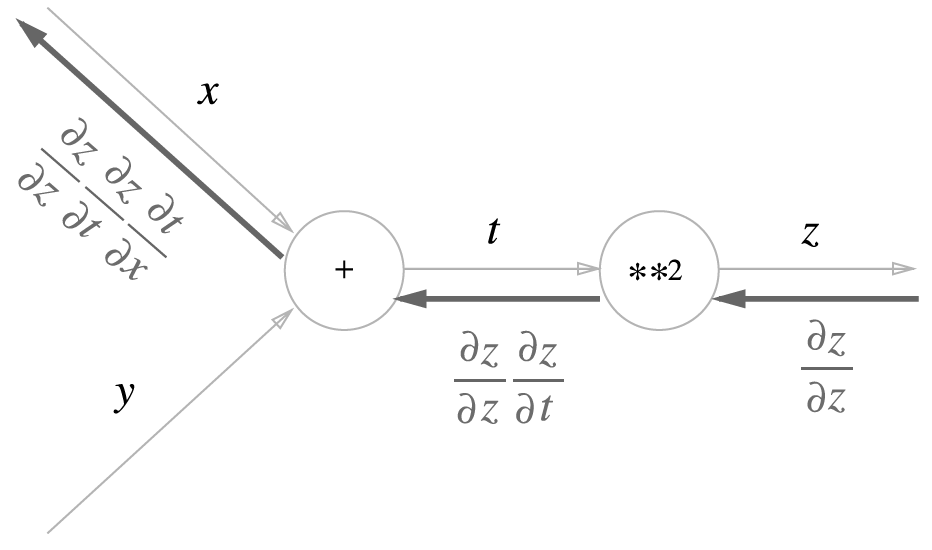
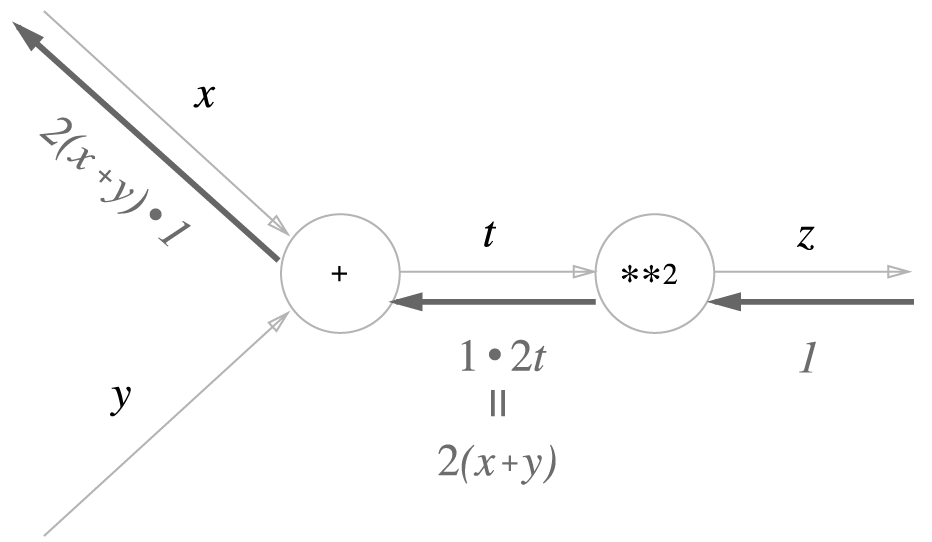
computational graph의 역전파 결과에 따르면 dz/dx는 2(x + y)가 된다
역전파
- 계산 그래프의 역전파가 연쇄법칙에 따라 진행되는 모습 설명
- '+'와 'x' 등의 예를 들어 역전파의 구조 설명
덧셈 노드의 역전파
z = x + y
덧셈 노드의 역전파 : 왼쪽이 순전파, 오른쪽이 역전파다. 덧셈노드의 역전파는 입력값을 그대로 흘려보낸다

최종 출력으로 가는 계산의 중간에 덧셈 노드가 존재한다.역전파에서는 국소적 미분이 가장 오른쪽의 출력에서 시작하여 노드를 타고 역방향(왼쪽)으로 전파된다
덧셈 노드 역전파의 구체적인 예 - 그대로 다음 노드로 전달

곱셈 노드의 역전파 z = xy
x에 대한 편미분 : y
y에 대한 편미분 : x
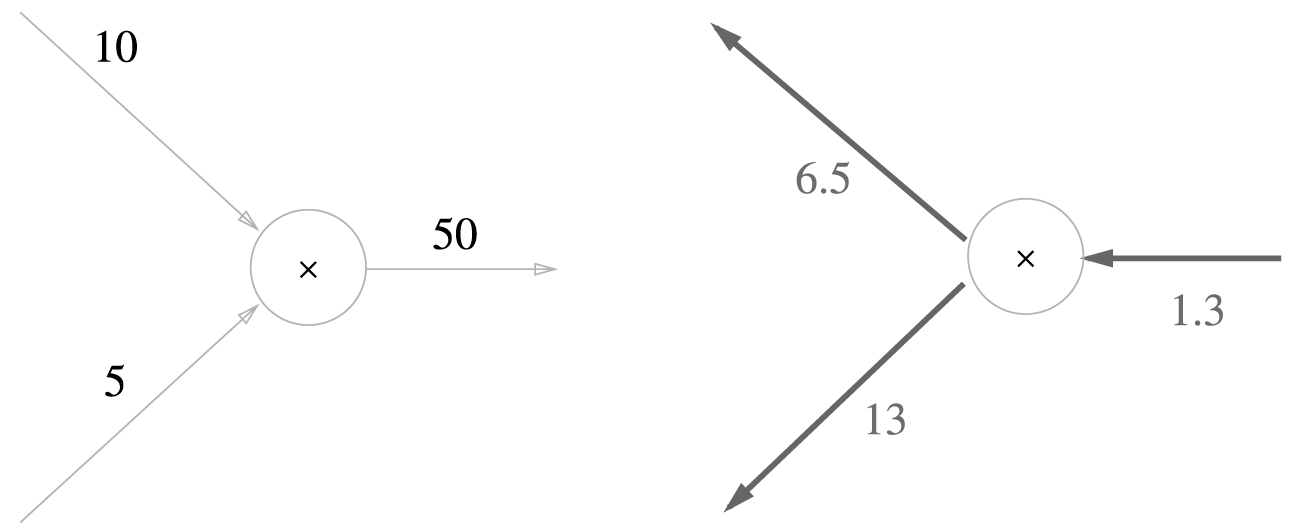
곱셈 노드 역전파의 구체적인 예

곱셈 노드 역전파의 구체적인 예
1.3 x 10 = 13 1.3 x 5 = 6.5
사과 쇼핑의 예
사과 쇼핑의 역전파 예

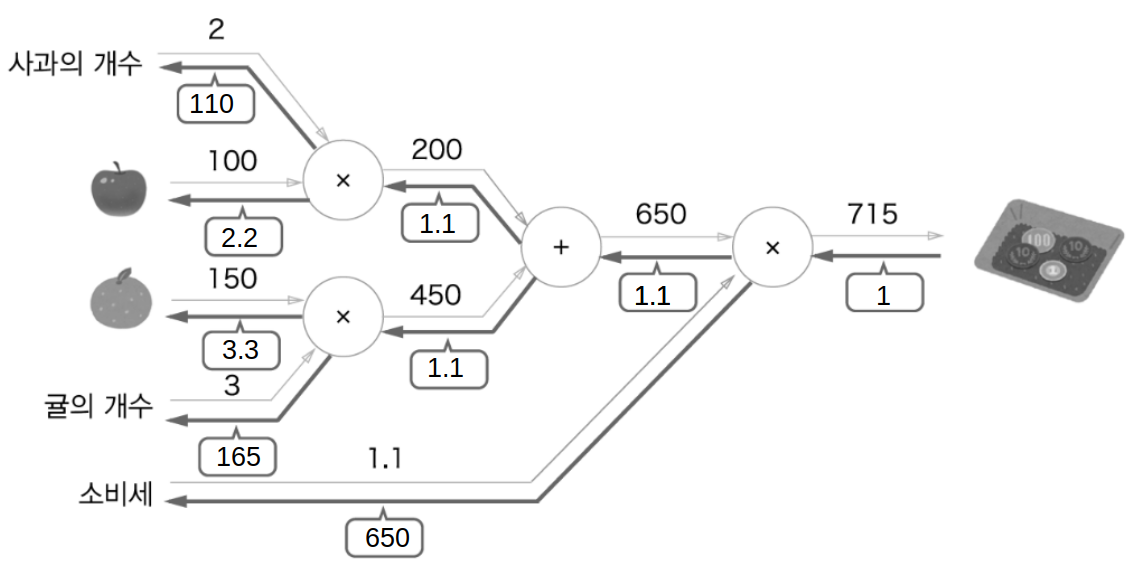
단순한 계층 구현하기
곱셈계층
# 곱셈 계층
'''
역전파가 구현된 곱셈 레이어 클래스
'''
class MulLayer: # (x * y)
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # 입력 받은 값에 x에 대한 편미분 값인 y를 곱하여 x 노드로 보낸다.
dy = dout * self.x # 입력 받은 값에 y에 대한 편미분 값인 x를 곱하여 y 노드로 보낸다.
return dx, dy
'''
위의 클래스를 사용하여 100원짜리 사과 2개를 사고 10%의 부가세가 포함된 그래프의 기울기를 구함.
'''
apple = 100 # 사과 가격 : 100
apple_num = 2 # 사과 개수 : 2
tax = 1.1 # 부가세 10%
# Layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num) # (1) 100원짜리 사과 2개 구매 -> 100 * 2
price = mul_tax_layer.forward(apple_price, tax) # (4) 10%의 부가세를 부여함. ((100 * 2) + (150 * 3)) * 1.1
# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice) # (4) 부가세의 기울기와 사과와 오렌지의 가격에 대한 기울기를 구함.
dapple, dapple_num = mul_apple_layer.backward(dapple_price) # (1) 개당 사과 가격과 사과 가격에 대한 기울기를 구함.
# print
# 구한 기울기 값들 출력
print("price:", int(price))
print("Apple gradient:", dapple)
print("Apple_num gradient:", int(dapple_num))
print("Tax gradient:", dtax)덧셈 계층
class AddLayer: # (x + y)
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1 # 입력 받은 값에 x에 대한 편미분 값인 1을 곱하여 x 노드로 보낸다.
dy = dout * 1 # 입력 받은 값에 y에 대한 편미분 값인 1을 곱하여 y 노드로 보낸다.
return dx ,dy
'''
위의 클래스를 사용하여 100원짜리 사과 2개와 150원짜리 오렌지 3개를 사고 10%의 부가세가 포함된 그래프의 기울기를 구함.
'''
apple = 100 # 사과 가격 : 100
apple_num = 2 # 사과 개수 : 2
orange = 150 # 오렌지 가격 : 150
orange_num = 3 # 오렌지 개수 : 3
tax = 1.1 # 부가세 10%
# Layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num) # (1) 100원짜리 사과 2개 구매 -> 100 * 2
orange_price = mul_orange_layer.forward(orange, orange_num) # (2) 150원짜리 오렌지 3개 구매 -> 150 * 3
all_price = add_apple_orange_layer.forward(apple_price, orange_price) # (3) 구매한 사과와 오렌지의 가격을 더함 (100 * 2) + (150 * 3)
price = mul_tax_layer.forward(all_price, tax) # (4) 10%의 부가세를 부여함. ((100 * 2) + (150 * 3)) * 1.1
# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice) # (4) 부가세의 기울기와 사과와 오렌지의 가격에 대한 기울기를 구함.
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) # (3) 사과의 가격과 오렌지의 가격에 대한 기울기를 구함.
dorange, dorange_num = mul_orange_layer.backward(dorange_price) # (2) 개당 오렌지 가격과 오렌지 개수에 대한 기울기를 구함.
dapple, dapple_num = mul_apple_layer.backward(dapple_price) # (1) 개당 사과 가격과 사과 가격에 대한 기울기를 구함.
# print
# 구한 기울기 값들 출력
print("price:", int(price))
print("Apple gradient:", dapple)
print("Apple_num gradient:", int(dapple_num))
print("Orange gradient:", dorange)
print("Orange_num gradient:", int(dorange_num))
print("Tax gradient:", dtax)
활성화 함수 계층 구현하기
ReLU 계층
ReLU 계층의 계산 그래프

class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0) # 0 - true 혹은 false로 저장 : 0 보다 작거나 같으면 true, 0 보다 크면 false,
out = x.copy() # for문 사용하지 않고 효율적으로 계산하기 위해
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
mask에 대하여
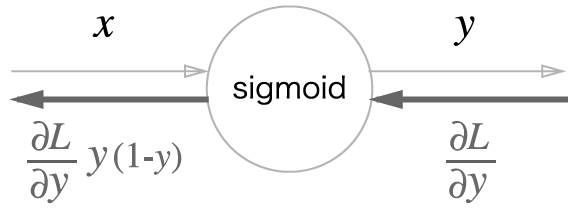
Sigmoid 계층
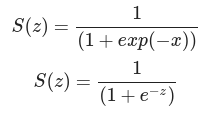
Sigmoid 계층의 계산 그래프(순전파)

- y = 1/x
- y' = -(1/x^2) = - y^2

2단계
- 덧셈 미분
- 1 * 상위단

3단계
- y = exp(x)
- y' = exp(x)
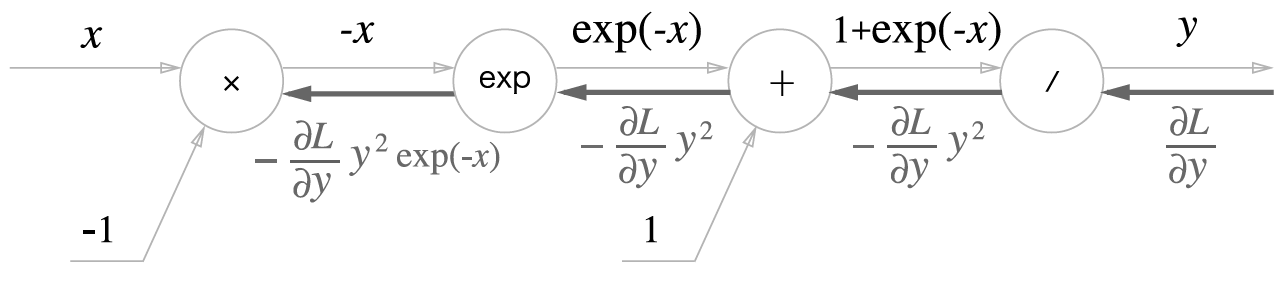
Sigmoid 계층의 계산 그래프
- 곱셈노드

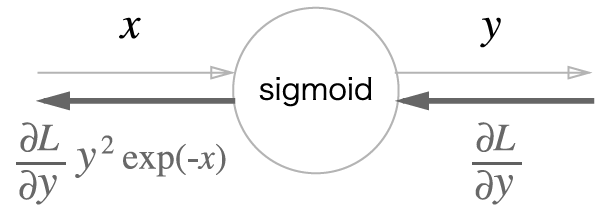
class sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1/(1+np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
Affine/Softmax 계층 구현하기
Affine 계층
X = np.random.rand(2) # 입력
W = np.random.rand(2, 3) # 가중치
B = np.random.rand(3) # 편향
print(X.shape)
print(W.shape)
print(B.shape)
Y = np.dot(X, W) + B
print(Y.shape)
print(Y)
행렬의 내적에서는 대응하는 차원의 원소 수를 일치시킨다

Affine 계층의 계산 그래프 : 변수가 행렬임에 주의. 각 변수의 형상을 변수명 위에 표기 했다

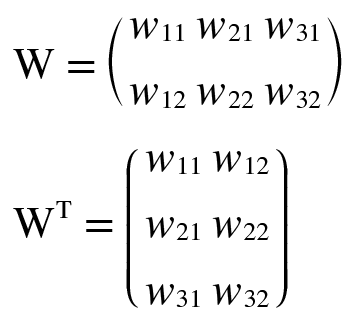
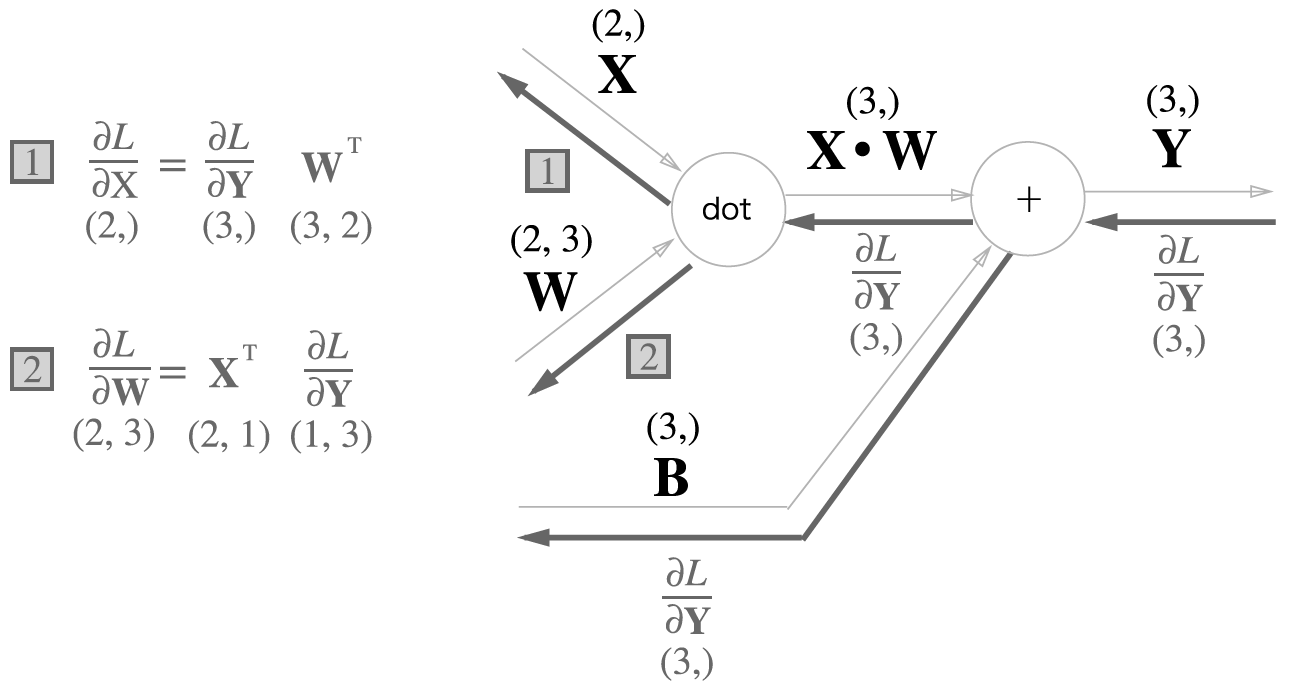
Affine 계츠의 역전파 : 변수가 다차원 배열임에 주의. 역전파에서의 변수 형상은 해당 변수명 아래에 표기했다
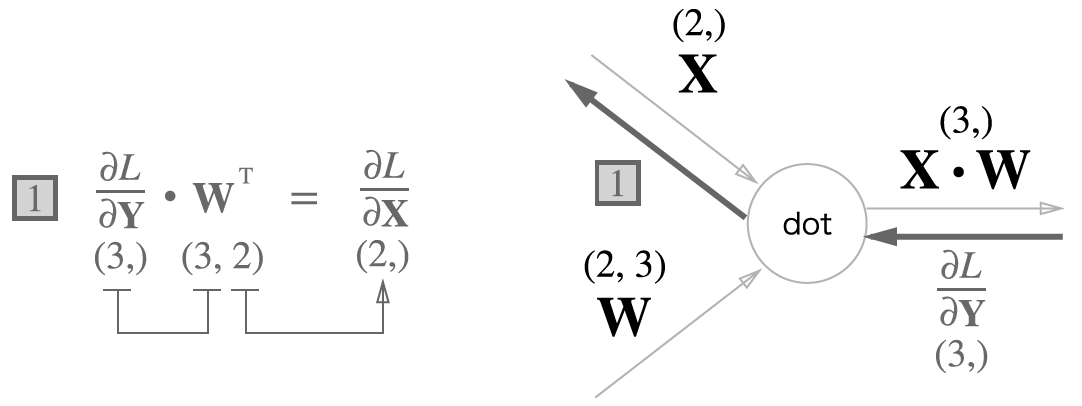
행렬 내적('dot' 노드)의 역전파는 행렬의 대응하는 차원의 원소 수가 일치하도록 내적을 조립하여 구할 수 있다
배치용 Affine 계층의 계산 그래프
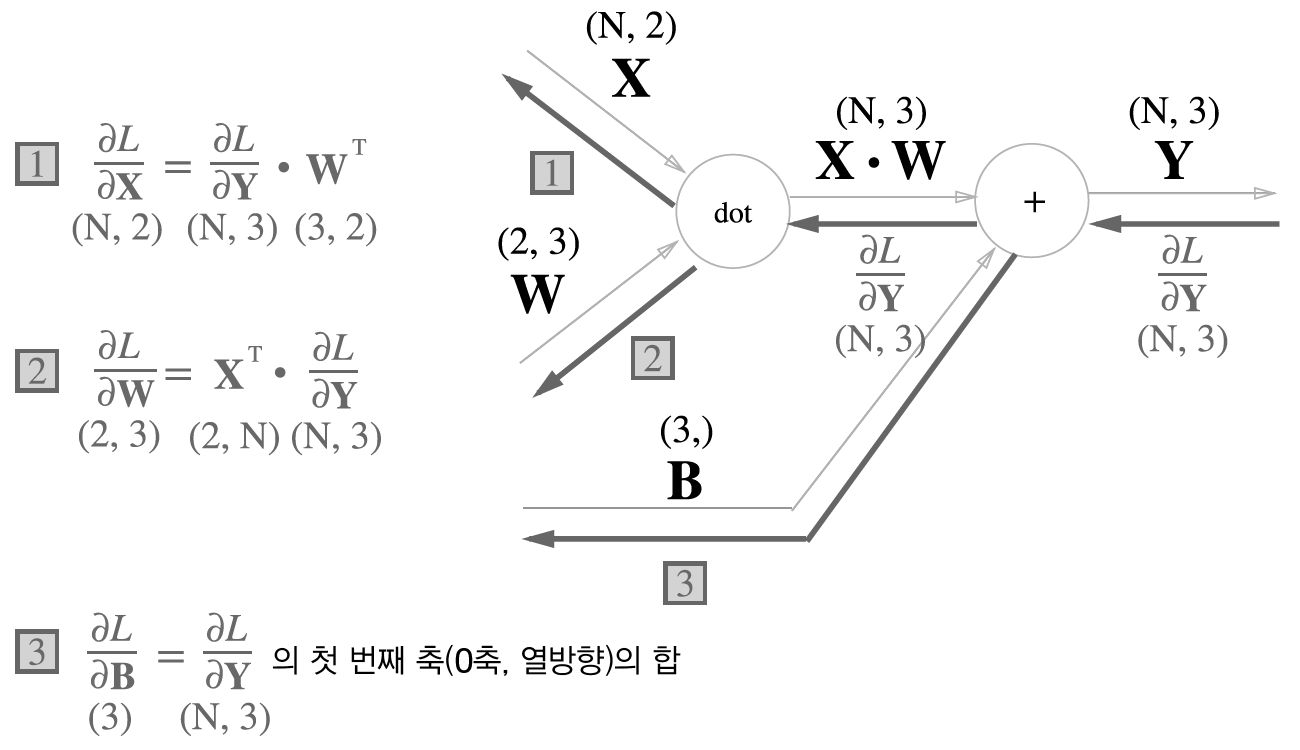
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 가중치와 편향 매개변수의 미분
self.dW = None
self.db = None
def forward(self, x):
# 텐서 대응
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 입력 데이터 모양 변경(텐서 대응)
return dx

class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실함수
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 인코딩 형태)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 정답 레이블이 원-핫 인코딩 형태일 때
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx오차역전파법을 사용한 학습 방법
위의 역전파를 사용한 기울기(Gradient) 값을 얻고 4장에서 배운 경사하강법(Gradient Descent)을 이용하여 레이어의 가중치들을 학습할 수 있다
'''
MNIST Dataset을 다운 받기 위한 셀로 볼 필요 없습니다.
mnist_load()로 사용하면 됩니다.
'''
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img':'train-images-idx3-ubyte.gz',
'train_label':'train-labels-idx1-ubyte.gz',
'test_img':'t10k-images-idx3-ubyte.gz',
'test_label':'t10k-labels-idx1-ubyte.gz'
}
dataset_dir = os.path.dirname(os.path.abspath(''))
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
"""MNIST 데이터셋 읽기
Parameters
----------
normalize : 이미지의 픽셀 값을 0.0~1.0 사이의 값으로 정규화할지 정한다.
one_hot_label :
one_hot_label이 True면、레이블을 원-핫(one-hot) 배열로 돌려준다.
one-hot 배열은 예를 들어 [0,0,1,0,0,0,0,0,0,0]처럼 한 원소만 1인 배열이다.
flatten : 입력 이미지를 1차원 배열로 만들지를 정한다.
Returns
-------
(훈련 이미지, 훈련 레이블), (시험 이미지, 시험 레이블)
"""
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])'''
신경망 구성을 위한 함수와 클래스 구현.
'''
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 가중치와 편향 매개변수의 미분
self.dW = None
self.db = None
def forward(self, x):
# 텐서 대응
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 입력 데이터 모양 변경(텐서 대응)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실함수
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 인코딩 형태)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 정답 레이블이 원-핫 인코딩 형태일 때
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dxfrom collections import OrderedDict
import matplotlib.pyplot as plt
import tensorflow as tf
'''
4장에서 구현한 2층 신경망을 오차역전파법을 사용하여 학습을 구현함.
'''
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
# Affine1 -> Relu1 -> Affine2 -> Softmax 의 레이어를 갖는 신경망을 구현.
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1 # 역전파의 초기 신호를 1으로 설정,
dout = self.lastLayer.backward(dout) # 역전파를 계산하여 해당 레이어 클래스에 기울기(Gradient)를 저장.
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = tf.keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000,-1) #flatten (60000,28,28) - > (60000,784)
x_train = x_train.astype('float32') / 255.
x_test = x_test.reshape(10000,-1)
x_test = x_test.astype('float32') / 255.
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.gradient(x_batch, t_batch)
# 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key] # 학습 후 계산한 기울기(Gradient)로 경사하강법을 사용하여 학습.
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch :", int(i / iter_per_epoch))
print("train_acc : %.4f" % (train_acc))
print("test_acc : %.4f" % (test_acc))
print()
# draw acc graph.
x = np.arange(1, len(train_acc_list) + 1)
plt.plot(x, train_acc_list, label='train Acc')
plt.plot(x, test_acc_list, label='test Acc', linestyle='--')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim(0, 1.0)
plt.legend(loc="lower right")
plt.show()
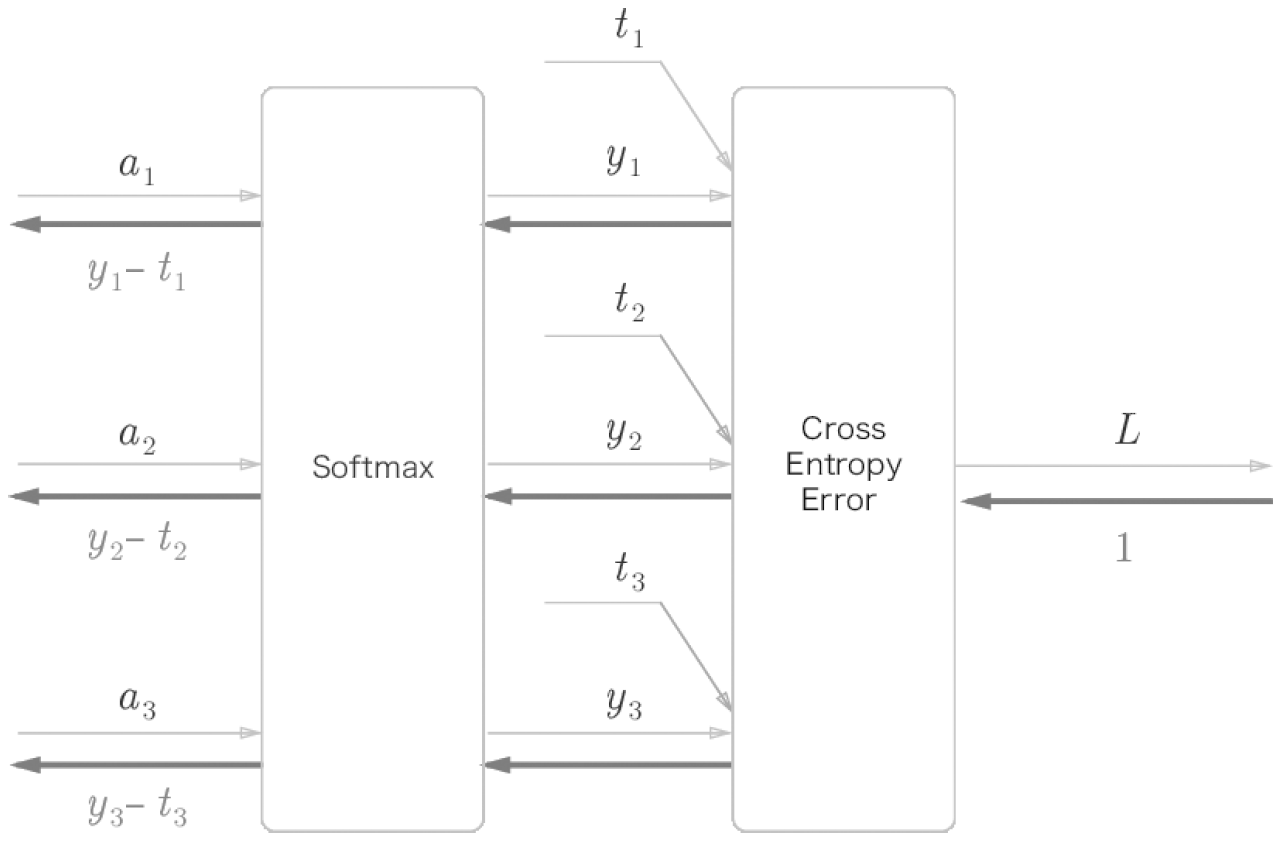
Softmax-with-Loss 계층의 계산 그래프
이전 계층으로부터 의 입력은 (a1, a2, a3)이며
Softmax 계층은 (Yl, Y2, Y3) 출력
정답 레이블은 (t1, t2, t3) 출력
Cross Entropy Error 계층은 손실 L 출력
Softmax-with-Loss 계층의 역전파 결과 (Yl - t1, Y2 - t2, Y3 - t3)
순전파
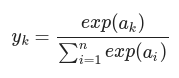
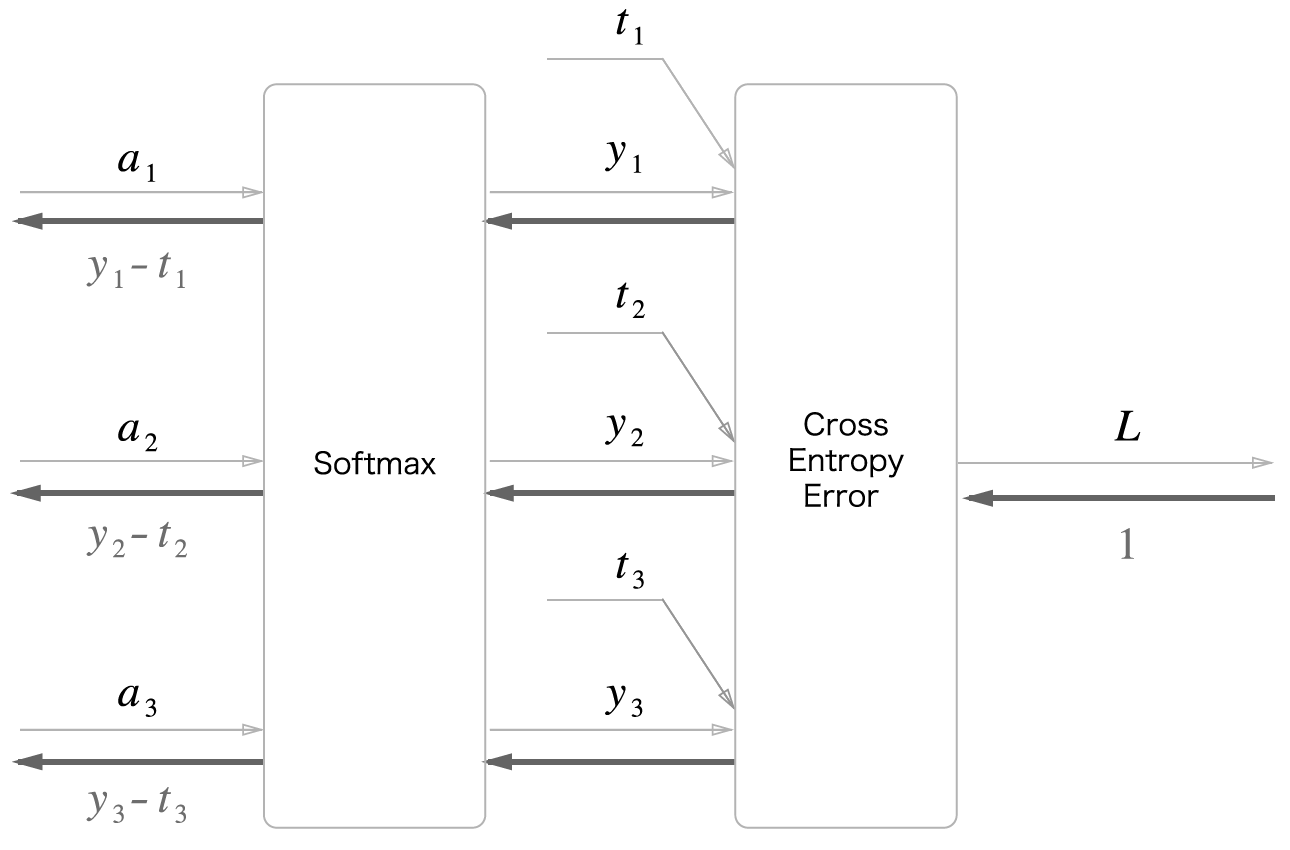
Softmax 계층의 계산 그래프(순전파만)


Cross Entropy Error 계층의 계산 그래프(순전파만)

역전파
Cross Entropy Error 계층의 역전파


1 단계

2 단계

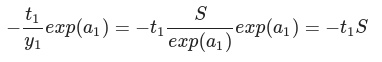
3 단계
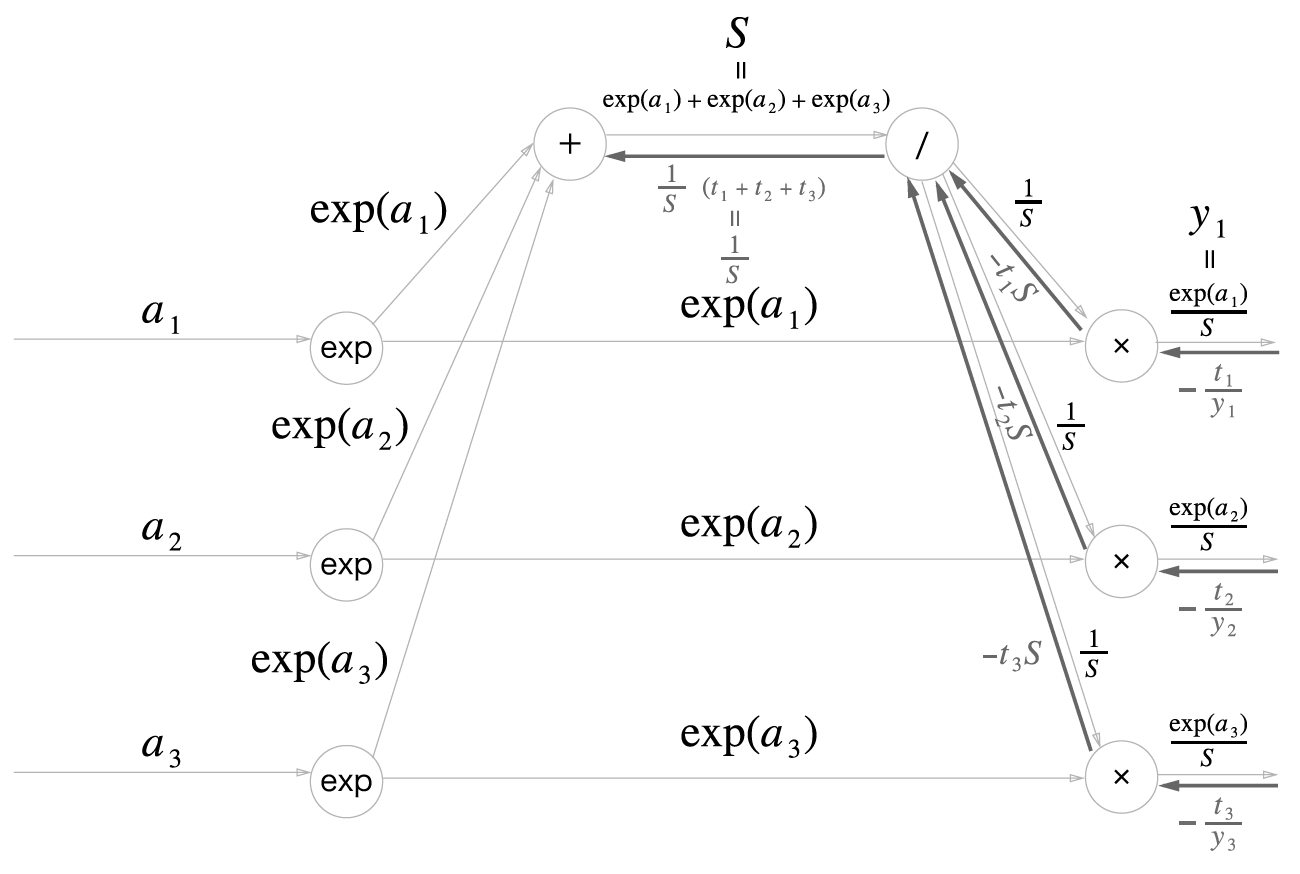
순전파 때 여러 갈래로 나뉘어 흘렸다면 역전파 때는그 반대로 흘러온 여러 값을 더함
3 개의 갈라진 역전파의 값 (−t1S, −t2S, −t3S) 이 더해짐
더해진 값에 /의 역전피를 하므로 1S(t1+t2+t3) 임
여기에서 (t1, t2, t3) 은 '원-핫 벡터'로 표현된 정답 레이블임
원-핫 벡터란 (t1, t2, t3) 중 단 하나만 1 이고 나머지는 전부 O 임을 뜻함
따라서 t1 + t2 + t3 = 1 이 됨
4 단계

5 단계
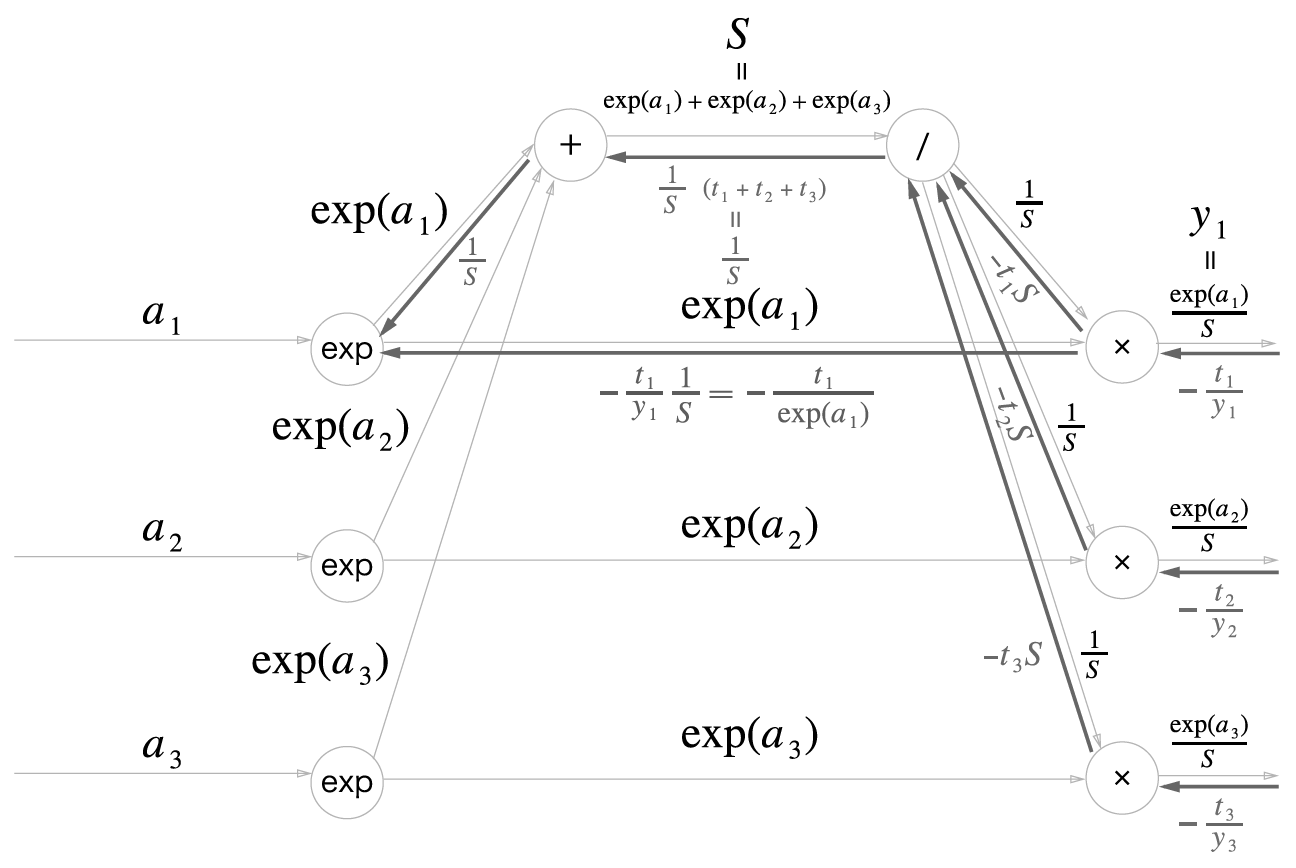
6 단계
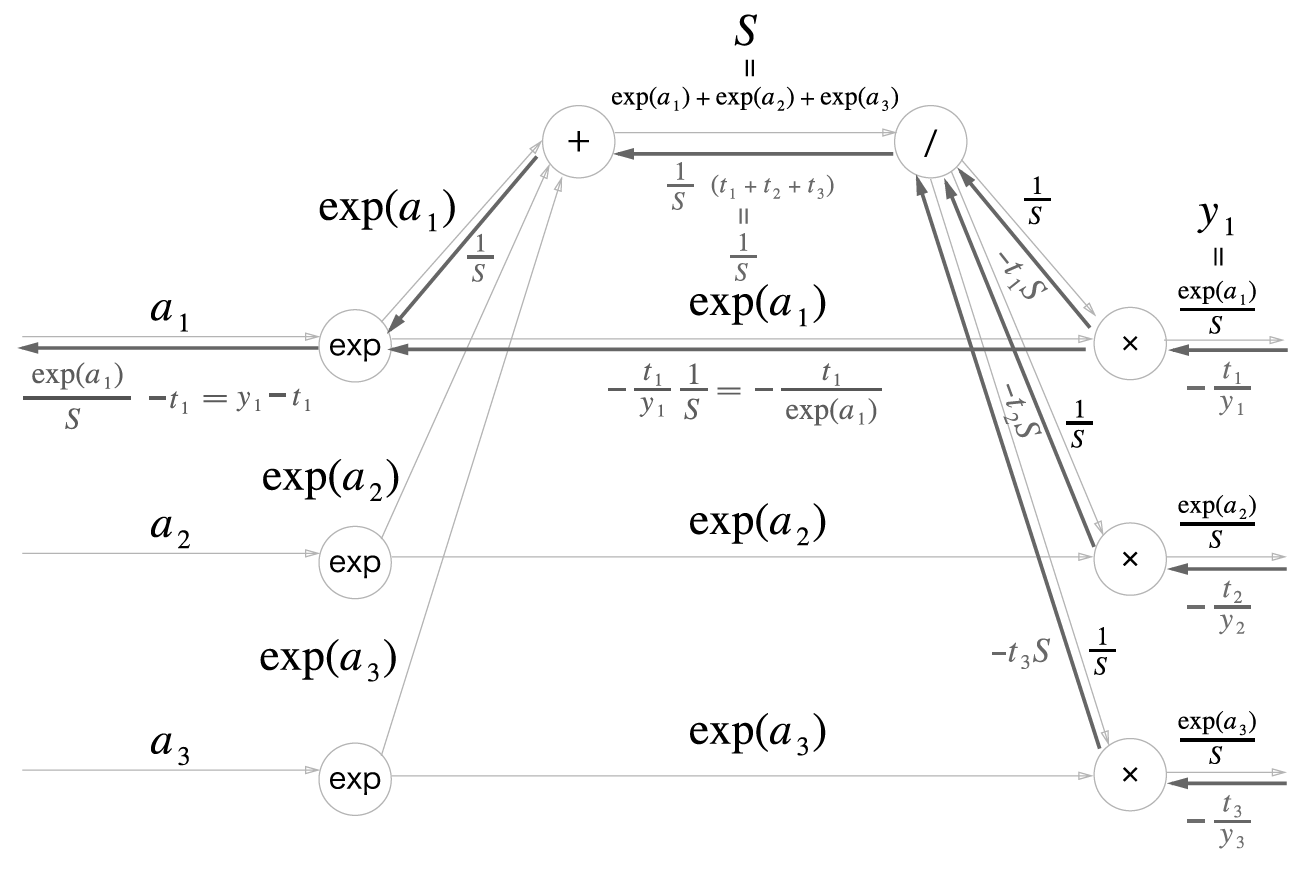
정리
Softmax-with-Loss 계층의 계산 그래프

'(두산로보틱스) ROKEY 부트 캠프 > Computer Vision 교육' 카테고리의 다른 글
| ep.43 합성곱 신경망(CNN) (0) | 2024.09.05 |
|---|---|
| ep.42 학습관련기술들 (0) | 2024.09.04 |
| ep.40 퍼셉트론, 신경망 (0) | 2024.09.02 |
| ep.39 OpenCV5 (0) | 2024.08.30 |
| ep.38 OpenCV4 (0) | 2024.08.29 |




