printf("ho_tari\n");
ep.29 딥러닝개론3 본문
2024.8.16
일차 함수, 기울기와 y 절편
▪ 함수란 두 집합 사이의 관계를 설명하는 수학 개념
▪ 변수 x와 y가 있을 때, x가 변하면 이에 따라 y는 어떤 규칙으로 변하는지 나타냄
▪ 보통 함수를 나타낼 때는 function의 f와 변수 x를 사용해 y =f(x)라고 표시
▪ 일차 함수는 y가 x에 관한 일차식으로 표현된 경우를 의미
▪ 예를 들어 다음과 같은 함수식으로 나타낼 수 있음
▪ x가 일차인 형태이며 x가 일차로 남으려면 a는 0이 아니어야 함
▪ 일차 함수식 y = ax + b에서 a는 기울기, b는 절편이라고 함
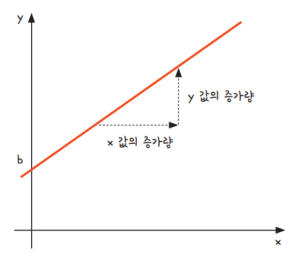
▪ 기울기는 기울어진 정도를 의미하는데, 그림 3-1에서 x 값이 증가할 때 y 값이 어느 정도 증가하는지에 따라 그래프의 기울기 a가 정해짐
▪ 절편은 그래프가 축과 만나는 지점을 의미
▪ 딥러닝의 수학 원리를 배울 때 초반부터 이 식이 등장
▪ x가 주어지고 원하는 y 값이 있을 때 적절한 a와 b를 찾는 것, 이것이 바로 딥러닝을 설명하는 가장 간단한 표현
이차 함수와 최솟값
▪ 이차 함수란 y가 x에 관한 이차식으로 표현되는 경우를 의미
▪ 다음과 같은 함수식으로 표현할 수 있음
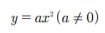
▪ 이차 함수의 그래프는 그림 3-2와 같이 포물선 모양
▪ a > 0이면 아래로 볼록한 그래프가 됨

▪ y = ax2의 그래프를 x축 방향으로 p만큼, y축 방향으로 q만큼 평행 이동시키면 그림 3-3과 같이 움직임
▪ 점 p와 q를 꼭짓점으로 하는 포물선이 됨
▪ 이때 포물선의 맨 아래에 위치한 지점이 최솟값이 되는데, 딥러닝을 실행할 때는 이 최솟값을 찾아내는 과정이 매우 중요함

▪ 이 최솟값은 4장에 소개할 ‘최소 제곱법’ 공식으로 쉽게 알아낼 수 있음
▪ 딥러닝을 실제로 실행할 때 만나는 문제에서는 대부분 최소 제곱법을 활용할 수가 없음
▪ 그 이유는 최소 제곱법을 계산하기 위해 꼭 필요한 조건들을 알 수 없기 때문임
▪ 미분과 기울기를 이용해야 함
미분, 순간 변화율과 기울기
▪ 딥러닝을 이해하는 데 가장 중요한 수학 원리는 미분이라고 할 수 있음
▪ 조금 전 딥러닝은 결국 일차 함수의 a와 b 값을 구하는 것인데, a와 b 값은 이차 함수 포물선의 최솟값을 구하는 것
▪ 이 최솟값을 미분으로 구하기 때문에 미분이 딥러닝에서 중요한 것
▪ 미분을 한다는 것은 쉽게 말해 이 ‘순간 변화율’을 구한다는 것
▪ 어느 순간에 어떤 변화가 일어나고 있는지 숫자로 나타낸 것을 미분 계수라고 하며, 이 미분 계수는 곧 그래프에서의 기울기를 의미
▪ 이 기울기가 중요한 것은 기울기가 0일 때, 즉 x축과 평행한 직선으로 그어질 때가 바로 그래프에서 최솟값인 지점이 되기 때문임

▪ 이 그래프에서 x 값의 증가량은 b -a이고, y 값의 증가량은 f(b) - f(a)
▪ 이를 Δ를 써서 표현하면 x 값의 증가량은 Δx로, y 값의 증가량은 f(a + Δx ) - f(a)로 나타낼 수 있음
▪ 직선의 기울기는 (y의 즐가량 / x의 증가량) 이라고 했음
▪ A와 B를 지나는 직선의 기울기는 다음과 같이 표현할 수 있음

▪ 이때 직선 AB의 기울기를 A와 B 사이의 ‘평균 변화율’이라고도 함
▪ 미분을 배우고 있는 우리에게 필요한 것은 순간 변화율
▪ 순간 변화율은 x의 증가량(Δx)이 0에 가까울 만큼 아주 작을 때의 순간적인 기울기를 의미하므로, 극한(limit) 기호를 사용해 다음과 같이 나타냄



편미분
▪ 미분과 더불어 딥러닝을 공부할 때 가장 자주 접하게 되는 또 다른 수학 개념은 바로 편미분
▪ 미분과 편미분 모두 ‘미분하라’는 의미에서는 다를 바가 없음
▪ 여러 가지 변수가 식 안에 있을 때, 모든 변수를 미분하는 것이 아니라 우리가 원하는 한 가지 변수만 미분하고 그 외에는 모두 상수로 취급하는 것이 바로 편미분
▪ 여기에는 변수가 x와 y, 이렇게 두 개 있음
▪ 이 중 어떤 변수로 미분해야 하는지 정해야 하므로 편미분을 사용하는 것
▪ 만일 이 식처럼 여러 변수 중에서 x에 관해서만 미분하고 싶다면, 함수 f를 ‘x에 관해 편미분하라’고 하며 다음과 같이 식을 씀
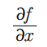
▪ 앞에 나온 함수 f(x, y) = x2 + yx + a를 x에 관해 편미분하는 과정은 어떻게 될까?
▪ 먼저 바로 앞에서 배운 미분의 성질 4에 따라 x2항은 2x가 됨
▪ 미분법의 기본 공식 3에 따라 yx는 y가 됨
▪ 마지막 항 a는 미분의 성질 1에 따라 0이 됨
▪ 이를 정리하면 다음과 같이 나타낼 수 있음
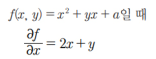
시그모이드 함수
▪ 딥러닝의 내부를 보면 입력받은 신호를 얼마나 출력할지를 계산하는 과정이 무수히 반복
▪ 이때 출력 값으로 얼마나 내보낼지를 계산하는 함수를 활성화 함수라고 함
▪ 활성화 함수는 딥러닝이 발전함에 따라 여러 가지 형태로 개발되어 왔는데, 그중 가장 먼저 배우는 중요한 함수가 바로 시그모이드 함수
▪ 시그모이드 함수는 지수 함수에서 밑 값이 자연 상수 e인 함수를 의미
▪ 자연 상수 e는 ‘자연 로그의 밑’, ‘오일러의 수’ 등 여러 이름으로 불리는데, 파이(π)처럼 수학에서 중요하게 사용되는 무리수이며 그 값은 대략 2.718281828…
▪ 자연 상수 e가 지수 함수에 포함되어 분모에 들어가면 시그모이드 함수가 되는데, 이를 식으로 나타내면 다음과 같음
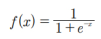
로그와 로그 함수
▪ 로그를 이해하려면 먼저 지수부터 이해해야 함
▪ a를 x만큼 거듭제곱한 값이 b라고 할 때, 이를 식으로 나타내면 다음과 같음

▪ 이때 a와 b를 알고 있는데 x를 모른다고 해 보자
▪ x는 과연 어떻게 구할 수 있을까?
▪ 이 x를 구하기 위해 사용하는 방법이 로그
▪ 영어로 Logarithm이라고 하는데 앞 세 글자 log를 사용해서 표시하며, 지수식에서 a와 b의 위치를 다음과 같이 바꾸어 쓰면 됨
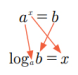
▪ 로그가 지수와 이렇게 밀접한 관계가 있듯이 로그 함수 역시 지수 함수와 밀접한 관계에 있음
▪ 바로 역함수의 관계
▪ 역함수는 x와 y를 서로 바꾸어 가지는 함수
▪ 지수 함수 y = ax(a ≠ 1, a > 0)는 로그 정의를 따라 x = logay로 바꿀 수 있음
▪ 역함수를 만들기 위해 x와 y를 서로 바꾸어 주면 됨
선형 회귀의 정의
▪ 독립 변수가 x 하나뿐이어서 이것만으로 정확히 설명할 수 없을 때는 x1, x2, x3 등 x 값을 여러 개 준비해 놓을 수도 있음
▪ 하나의 x 값만으로도 y 값을 설명할 수 있다면 단순 선형 회귀(simple linear regression)라고 함
▪ 또한, x 값이 여러 개 필요하다면 다중 선형 회귀(multiple linear regression)라고 함
가장 훌륭한 예측선이란?
▪ 좌표 평면에 나타내 놓고 보니, 왼쪽이 아래로 향하고 오른쪽이 위를 향하는 일종의 ‘선형(선으로 표시될 만한 형태)’을 보임
▪ 선형 회귀를 공부하는 과정은 이 점들의 특징을 가장 잘 나타내는 선을 그리는 과정과 일치
▪ 여기서 x 값은 독립 변수이고 y 값은 종속 변수
▪ 즉, x 값에 따라 y 값은 반드시 달라짐
▪ 다만, 정확하게 계산하려면 상수 a와 b의 값을 알아야 함
▪ 이 직선을 훌륭하게 그으려면 직선의 기울기 a 값과 y 절편 b 값을 정확히 예측해 내야 함
▪ 앞서 선형 회귀는 곧 정확한 선을 그려 내는 과정이라고 했음
▪ 지금 주어진 데이터에서의 선형 회귀는 결국 최적의 a 값과 b 값을 찾아내는 작업이라고 할 수 있음
최소 제곱법
▪ 이제 우리 목표는 가장 정확한 선을 긋는 것
▪ 더 구체적으로는 정확한 기울기 a와 정확한 y 절편 b를 알아내면 된다고 했음
▪ 만일 우리가 최소 제곱법(method of least squares)이라는 공식을 알고 적용한다면, 이를 통해 일차 함수의 기울기 a와 y 절편 b를 바로 구할 수 있음
평균 제곱 오차
▪ 최소 제곱법을 이용해 기울기 a와 y 절편을 편리하게 구했지만, 이 공식만으로 앞으로 만나게 될 모든 상황을 해결하기는 어려움
▪ 여러 개의 입력을 처리하기에는 무리가 있기 때문임
▪ 예를 들어 앞서 살펴본 예에서는 변수가 ‘공부한 시간’ 하나뿐이지만, 2장에서 살펴본 폐암 수술 환자의 생존율 데이터를 보면 입력 데이터의 종류가 17개나 됨
▪ 딥러닝은 대부분 입력 값이 여러 개인 상황에서 이를 해결하기 위해 실행되기 때문에 기울기 a와 y 절편 b를 찾아내는 다른 방법이 필요함
▪ 가장 많이 사용하는 방법은 ‘일단 그리고 조금씩 수정해 나가기’ 방식
▪ 가설을 하나 세운 후 이 값이 주어진 요건을 충족하는지 판단해서 조금씩 변화를 주고, 이 변화가 긍정적이면 오차가 최소가 될 때까지 이 과정을 계속 반복하는 방법
▪ 이는 딥러닝을 가능하게 하는 가장 중요한 원리 중 하나
▪ 선을 긋고 나서 수정하는 과정에서 빠지면 안 되는 것이 있음
▪ 나중에 그린 선이 먼저 그린 선보다 더 좋은지 나쁜지를 판단하는 방법
▪ 즉, 각 선의 오차를 계산할 수 있어야 하고, 오차가 작은 쪽으로 바꾸는 알고리즘이 필요한 것
▪ 이를 위해 주어진 선의 오차를 평가하는 방법이 필요함
▪ 오차를 구할 때 가장 많이 사용되는 방법이 평균 제곱 오차(Mean Square Error, MSE)
▪ 오차에 양수와 음수가 섞여 있어 오차를 단순히 더해 버리면 합이 0이 될 수도 있기 때문임
▪ 부호를 없애야 정확한 오차를 구할 수 있음
▪ 오차의 합을 구할 때는 각 오차 값을 제곱해 줌
▪ 이를 식으로 표현하면 다음과 같음

경사 하강법의 개요
▪ 경사 하강법은 이렇게 반복적으로 기울기 a를 변화시켜서 m값을 찾아내는 방법
▪ 여기서 우리는 학습률(learning rate)이라는 개념을 알 수 있음
▪ 기울기의 부호를 바꾸어 이동시킬 때 적절한 거리를 찾지 못해 너무 멀리 이동시키면 a 값이 한 점으로 모이지 않고 그림 5-4와 같이 위로 치솟아 버림

▪ 어느 만큼 이동시킬지 신중히 결정해야 하는데, 이때 이동 거리를 정해 주는 것이 바로 학습률
▪ 딥러닝에서 학습률의 값을 적절히 바꾸면서 최적의 학습률을 찾는 것은 중요한 최적화 과정 중 하나
▪ 다시 말해 경사 하강법은 오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것
▪ y 절편 b의 값도 이와 같은 성질을 가지고 있음
▪ b 값이 너무 크면 오차도 함께 커지고, 너무 작아도 오차가 커짐
▪ 최적의 b 값을 구할 때 역시 경사 하강법을 사용
와인 데이터 분석

데이터 수집
• 캘리포니아 어바인 대학의 머신러닝 저장소에서 제공하는 오픈 데이터를 사용
https://archive.ics.uci.edu/dataset/186/wine+quality
UCI Machine Learning Repository
This dataset is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. This allows for the sharing and adaptation of the datasets for any purpose, provided that the appropriate credit is given.
archive.ics.uci.edu
데이터 준비
1. 다운로드한 CSV 파일 정리하기
• 엑셀은 CSV 파일을 열 때 쉼표를 열 구분자로 사용하므로 열이 깨진 것처럼 보임
• 엑셀에서 세미콜론을 열 구분자 로 인식하도록 파일을 다시 저장해야 함
1. 엑셀에서 열 구분자를 세미콜론으로 인식시키기
import pandas as pd
red_df = pd.read_csv('/content/drive/MyDrive/winequality-red.csv', sep = ';', header=0, engine='python')
white_df = pd.read_csv('/content/drive/MyDrive/winequality-white.csv', sep=';', header=0, engine='python')
red_df.to_csv('/content/drive/MyDrive/winequality-red2.csv', index = False)
white_df.to_csv('/content/drive/MyDrive/winequality-white2.csv', index = False)2. 파이썬에서 저장한 CSV 파일을 엑셀에서 열어 상태를 확인
2. 데이터 병합하기
1. 레드 와인과 화이트 와인 파일 합치기
red_df.head()
red_df.insert(0, column = 'type', value = 'red')
red_df.head()
red_df.shape
white_df.head()
white_df.insert(0, column = 'type', value = 'white')
white_df.head()
white_df.shape
wine = pd.concat([red_df, white_df])
wine.shape
wine.to_csv('/content/drive/MyDrive/wine.csv', index = False)• 01행 red_df에 저장된 내용을 위에서부터 5개(0번~4번) 행만 출력하여 확인
• 02행 이름이 ‘type’이고 값이 ‘red’인 열을 만들어 index = 0(첫 번째 열) 자리에 삽입
• 03행 red_df에 저장된 내용을 위에서부터 5개(0번~4번) 행만 다시 출력해 삽입된 ‘type’열을 확인
• 04행 red_df.shape를 이용하여 현재 red_df의 크기를 ‘(행의 개수, 열의 개수)’ 형태로 확인
• 05행 white_df에 저장된 내용을 위에서부터 5개(0번~4번) 행만 출력하여 확인
• 06행 이름이 ‘type’이고 값이 ‘white’인 열을 만들어 index = 0(첫 번째 열) 자리에 삽입
• 07행 white_df에 저장된 내용을 위에서부터 5개(0번~4번) 행만 다시 출력해 삽입된‘type’ 열을 확인
• 08행 white_df.shape를 이용하여 현재 white_df의 크기를 ‘(행의 개수, 열의 개수)’ 형태로 확인
• 09행 pd.concat() 함수를 이용하여 red_df와 white_df를 결합
• 10행 결합된 wine의 현재 크기를 ‘(행의 개수, 열의 개수)’ 형태로 확인
• 11행 wine을 CSV 파일로 저장



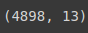
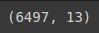
2. 결합된 파일 확인하기

데이터 탐색
1. 기본 정보 확인하기
print(wine.info())
• 전체 샘플은 6,497개이고 속성을 나타내는 열은 13개
• 각 속성의 이름은 type부터 quality까지
• 속성 중에서 실수 타입(float64)은 11개
• 정수 타입(int64)은 1개(quality), 객체 타입(object)이 1개(type)
• 독립 변수(x)는 type부터 alcohol 까지 12개, 종속 변수(y)는 1개(quality)
2. 함수를 사용해 기술 통계 구하기
wine.dolumns = wine.columns.str.replace('', '_')
wine.head()
wine.describe()
•[01~04행] 열이름 정렬하기
•01행 열 이름에 공백이 있으면 밑줄로 바꾼 뒤 한 단어로 연결
•02행 변경된 열 이름을 확인
•03행 describe() 함수를 사용하여 속성별 개수, 평균, 표준편차, 최소값,
•전체 데이터 백분율에 대한 25번째 백분위수(25%),
•중앙값인 50번째 백분위수(50%), 75번째 백분위수(75%)
•그리고 100번째 백분위수인 최대값max을 출력
sorted(wine.quality.unique())
wine.quality.value_counts()
• 04행 wine.quality.unique() 함수를 사용하여 quality 속성값 중에서 유일한 값을 출력
이를 통해 와인 품질 등급quality은 3, 4, 5, 6, 7, 8, 9의 7개 등급이 있다는 것을 알 수 있음
• 05행 quality.value_counts() 함수는 quality 속성값에 대한 빈도수를 보여줌
6등급인 샘플이 2,826개로 가장 많고, 9등급인 샘플이 5개로 가장 적은 것을 알 수 있음
데이터 모델링
1. describe() 함수로 그룹 비교하기
wine.groupby('type')['quality'].describe()
wine.groupby('type')['quality'].mean()
wine.groupby('type')['quality'].std()
wine.groupby('type')['quality'].agg(['mean', 'std'])
• 01행 레드 와인과 화이트 와인을 구분하는 속성인 type을 기준으로 그룹을 나눈 뒤 그룹 안에서 quality 속성을 기준으로 기술 통계를 구함
• 02~04행 기술 통계 전부를 구할 때는 describe() 함수를 사용하지만 mean() 함수로 평균만 구하거나 std() 함수로 표준편차만 따로 구할 수도 있음
mean() 함수와 std() 함수를 묶어서 한 번에 사용하려면 04행과 같이 agg() 함수를 사용
2. t-검정과 회귀 분석으로 그룹 비교하기
• t-검정을 위해서는 scipy 라이브러리 패키지를 사용
• 회귀 분석을 위해서는 statsmodels 라이브러리 패키지를 사용
• 명령 프롬프트 창에서 다음과 같이 입력하여 statsmodels 패키지를 설치
from scipy import stats
from statsmodels.formula.api import ols, glm
red_wine_quality = wine.loc[wine['type'] == 'red', 'quality']
white_wine_quality = wine.loc[wine['type'] == 'white', 'quality']
stats.ttest_ind(red_wine_quality, white_wine_quality, equal_var = False)
Rformula = 'quality ~ fixed_acidity + volatile_acidity + citric_acid + residual_sugar + chlorides + free_sulfur_dioxide + total_sulfur_dioxide + density + pH + sulphates + alcohol'
regression_result = ols(Rformula, data = wine).fit()
regression_result.summary()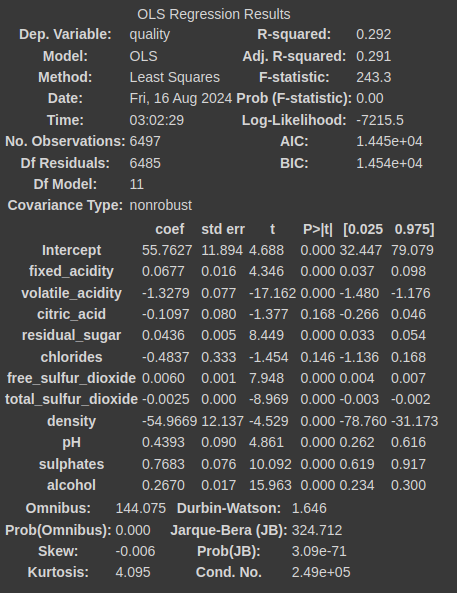
• [01~02행]
• t-검정에 필요한 scipy 패키지의 stats 함수와 회귀 분석에 필요한 statsmodels.formula.api 패키지의 ols, glm 함수를 로드
• [03~04행] 그룹 분리하기
• 03행 레드 와인 샘플의 quality 값만 찾아서 red_wine에 저장
• 04행 화이트 와인 샘플의 quality 값만 찾아서 white_wine에 저장
• 05행 scipy 패키지의 stats.ttest_ind() 함수를 사용하여 t-검정을 하고 두 그룹 간 차이를 확인
• [06~08행] 선형 회귀 분석 수행하기
• 06행 선형 회귀 분석식의 종속 변수(y)와 독립 변수(x1~x10)를 구성
• 07행 선형 회귀 모델 중에서 OLSOrdinary Least Squares 모델을 사용
• 08행 선형 회귀 분석과 관련된 통계값을 출력
3. 회귀 분석 모델로 새로운 샘플의 품질 등급 예측하기
sample1 = wine[wine.columns.difference(['quality', 'type'])]
sample1 = sample1[0:5][:]
sample1_predict = regression_result.predict(sample1)
sample1_predict
wine[0:5]['quality']
data = {"fixed_acidity" : [8.5, 8.1], "volatile_acidity":[0.8, 0.5],"citric_acid":[0.3, 0.4], "residual_sugar":[6.1, 5.8],"chlorides":[0.055,0.04], "free_sulfur_dioxide":[30.0, 31.0],"total_sulfur_dioxide":[98.0, 99], "density":[0.996, 0.91], "pH":[3.25, 3.01], "sulphates":[0.4, 0.35], "alcohol":[9.0, 0.88]}
sample2 = ample2 = pd.DataFrame(data, columns= sample1.columns)
sample2
sample2_predict = regression_result.predict(sample2)
sample2_predict
• [01~02행] 예측에 사용할 첫 번째 샘플 데이터 만들기
• 01행 wine에서 quality와 type 열은 제외하고, 회귀 분석 모델에 사용할 독립 변수만 추출하여 sample1에 저장
• 02행 sample1에 있는 샘플 중에서 0번~4번 5개 샘플만 추출하고, sample1에 다시 저장하여 예측에 사용할 샘플을 제작
• [03~05행] 첫 번째 샘플의 quality 예측하기
• 03행 샘플 데이터를 회귀 분석 모델 regression_result의 예측 함수 predict()에 적용하여 수행한 뒤 결과 예측값 sample1_predict에 저장
• 04행 sample1_predict를 출력하여 예측한 quality를 확인
• 05행 wine에서 0번부터 4번까지 샘플의 quality 값을 출력하여 sample1_predict이 맞게 예측되었는지 확인
• [06~08행] 예측에 사용할 두 번째 샘플 데이터 만들기
• 06행 회귀식에 사용한 독립 변수에 대입할 임의의 값을 딕셔너리 형태로 제작
• 07행 딕셔너리 형태의 값과 sample1의 열 이름만 뽑아 데이터프레임으로 묶은 sample2를 제작
• 08행 sample2를 출력하여 제대로 구성되었는지 확인
• [09~10행] 두 번째 샘플의 quality 예측하기
• 09행 샘플 데이터를 회귀 분석 모델 regression_result의 예측 함수 predict()에 적용하여 수행한 뒤 결과 예측값을sample2_predict에 저장
• 10행 sample2_predict를 출력하여 예측한 quality를 확인
결과 시각화
1. 와인 유형에 따른 품질 등급 히스토그램 그리기
1. 명령 프롬프트 창에서 다음 명령을 입력하여 seaborn 라이브러리 패키지를 설치 그 후 파이썬 셸 창으로 돌아와 임포트
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('dark')
sns.distplot(red_wine_quality, kde = True, color = 'red', label = 'red wine')
sns.distplot(white_wine_quality, kde = True, label = 'white wine')
plt.title("Quality of Wine Type")
plt.legend()
plt.show()
2. 부분 회귀 플롯으로 시각화하기
• 독립 변수가 2개 이상인 경우에는 부분 회귀 플롯을 사용하여 하나의 독립 변수가 종속 변수에 미치는 영향력을 시각화 함으로써 결과를 분석할 수 있음
import statsmodels.api as sm
others = list(set(wine.columns).difference(set(["quality", "fixed_acidity"])))
p, resids = sm.graphics.plot_partregress("quality", "fixed_acidity", others, data = wine, ret_coords = True)
plt.show()
fig = plt.figure(figsize = (8, 13))
sm.graphics.plot_partregress_grid(regression_result, fig = fig)
plt.show()

• 01행 부분 회귀 계산을 위해 statsmodels.api를 로드
• [02~04행] fixed_acidity가 종속 변수 quality에 미치는 영향력을 시각화하기
• 02행 부분 회귀에 사용한 독립 변수와 종속 변수를 제외한 나머지 변수 이름을 리스트 others로 추출
• 03행 나머지 변수는 고정하고 fixed_acidity가 종속 변수 quality에 미치는 영향에 부분회귀를 수행
• 04행 부분 회귀의 결과를 플롯으로 시각화하여 나타냄
• [05~07행] 각 독립 변수가 종속 변수 quality에 미치는 영향력을 시각화하기
• 05행 차트의 크기를 지정
• 06행 다중 선형 회귀 분석 결과를 가지고 있는 regression_result를 이용해 각 독립 변수의 부분 회귀 플롯을 구함
• 07행 부분 회귀 결과를 플롯으로 시각화하여 나타냄
파이썬 코딩으로 확인하는 선형 회귀
import numpy as np
import matplotlib.pyplot as plt
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])
a = 0
b = 0
lr = 0.03
epochs = 2001
n = len(x)
for i in range(epochs):
y_pred = a * x + b
error = y - y_pred
a_diff = (2/n) * sum(-x * (error))
b_diff = (2/n) * sum(-(error))
a = a - lr * a_diff
b = b - lr * b_diff
if i % 100 == 0:
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
y_pred = a * x + b
plt.scatter(x, y)
plt.plot(x, y_pred, 'r')
plt.show()

텐서플로에서 실행하는 선형 회귀, 다중 선형 회귀 모델
▪ 선형 회귀는 현상을 분석하는 방법의 하나
▪ 머신 러닝은 이러한 분석 방법을 이용해 예측 모델을 만드는 것
▪ 두 분야에서 사용하는 용어가 약간 다름
▪ 예를 들어 함수 y = ax + b는 공부한 시간과 성적의 관계를 유추하기 위해 필요했던 식
▪ 이렇게 문제를 해결하기 위해 가정하는 식을 머신 러닝에서는 가설 함수(hypothesis)라고 하며 H(x)라고 표기
▪ 또 기울기 a는 변수 x에 어느 정도의 가중치를 곱하는지 결정하므로, 가중치(weight)라고 하며, w로 표시
▪ 절편 b는 데이터의 특성에 따라 따로 부여되는 값이므로 편향(bias)이라고 하며, b로 표시
▪ 우리가 앞서 배운 y = ax + b는 머신 러닝에서 다음과 같이

▪ 또한, 평균 제곱 오차처럼 실제 값과 예측 값 사이의 오차에 대한 식을 손실 함수(loss function)라고 함
▪ 최적의 기울기와 절편을 찾기 위해 앞서 경사 하강법을 배웠음
▪ 딥러닝에서는 이를 옵티마이저(optimizer)라고 함
▪ 우리가 사용했던 경사 하강법은 딥러닝에서 사용하는 여러 옵티마이저 중 하나였음
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])
model = Sequential()
model.add(Dense(1, input_dim=1, activation='linear'))
model.compile(optimizer='sgd', loss='mse')
model.fit(x, y, epochs=200)
plt.scatter(x, y)
plt.plot(x, model.predict(x), 'r')
plt.show()
hour = np.array([7])
prediction = model.predict([hour])
print("%.f시간을 공부할 경우의 예상 점수는 %.02f점입니다." % (hour, prediction))
로지스틱 회귀의 정의
▪ 로지스틱 회귀는 선형 회귀와 마찬가지로 적절한 선을 그려 가는 과정
▪ 다만, 직선이 아니라 참(1)과 거짓(0) 사이를 구분하는 S자 형태의 선을 그어 주는 작업
텐서플로에서 실행하는 로지스틱 회귀 모델
▪ 텐서플로에서 실행하는 방법은 앞서 선형 회귀 모델을 만들 때와 유사함
▪ 다른 점은 오차를 계산하기 위한 손실 함수가 평균 제곱 오차 함수에서 크로스 엔트로피 오차로 바뀐다는 것
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
x = np.array([2, 4, 6, 8, 10, 12, 14])
y = np.array([0, 0, 0, 1, 1, 1, 1])
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))
model.compile(optimizer='sgd', loss='binary_crossentropy')
model.fit(x, y, epochs=200)
plt.scatter(x, y)
plt.plot(x, model.predict(x), 'r')
plt.show()
hour = 7
prediction = model.predict(np.array([hour]))
print("%.f시간을 공부할 경우, 합격 예상 확률은 %.01f%%입니다." % (hour, prediction * 100))
보스톤 주택 가격

• 데이터 수집, 준비 및 탐색
2. 데이터가 이미 정리된 상태이므로 데이터셋 구성을 확인
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
boston = fetch_california_housing()
print(boston.DESCR)
boston_df = pd.DataFrame(boston.data, columns = boston.feature_names)
boston_df.head()
boston_df['PRICE'] = boston.target
boston_df.head()
print("보스톤 주택 가격 데이터셋 크기: ", boston_df.shape)
boston_df.info()
분석 모델 구축, 결과 분석 및 시각화
1. 선형 회귀를 이용해 분석 모델 구축하기
1. 사이킷런의 선형 분석 모델 패키지sklearn.linear_model에서 선형 회귀LinearRegression를 이용하여 분석 모델을 구축
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
Y = boston_df['PRICE']
X = boston_df.drop(['PRICE'], axis = 1, inplace = False)
X_train, X_test, Y_test, Y_test = train_test_split(X, Y, test_size = 0.3, random_state = 156)
lr = LinearRegression()
lr.fit(X_train, Y_train)
Y_predict = lr.predict(X_test)- 사이킷런을 사용하여 머신러닝 회귀 분석을 하기 위한 LinearRegression과 데이터셋 분리 작업을 위한 train_test_split, 성능 측정을 위한 평가 지표인 mean_squared_ error, r2_score를 임포트
- PRICE 피처를 회귀식의 종속 변수 Y로 설정하고 PRICE를 제외 drop( )한 나머지 피처를 독립 변수 X로 설정
- X와 Y 데이터 506개를 학습 데이터와 평가 데이터로 7:3 비율로 분할test_size=0.3
- 선형 회귀 분석 모델 객체 lr을 생성
- 학습 데이터 XX_train와 YY_train를 가지고 학습을 수행fit( ).
- 평가 데이터 XX_test를 가지고 예측을 수행하여predict( ) 예측값YY_predict를 구함
2. 선형 회귀 분석 모델을 평가 지표를 통해 평가하고 회귀 계수를 확인하여 피처의 영향을 분석
mse = mean_squared_error(Y_test, Y_predict)
rmse = np.sqrt(mse)
print("MSE: {0:.3f}, RMSE: {1:.3f}".format(mse, rmse))
print('R^2(Variance score) : {0:.3f}'.format(r2_score(Y_test, Y_predict)))
print('Y 절편 값: ', lr.intercept_)
print('회귀 계수 값: ', np.round(lr.coef_, 1))
- 회귀 분석은 지도 학습이므로 평가 데이터 X에 대한 결과값 YY_test를 이미 알고 있는 상태에서 평가 데이터 YY_test와 구한 예측 결과Y_predict의 오차를 계산하여 모델을 평가. 평가 지표 MSE를 구하고mean_squared_error( ) 구한 값의 제곱근을 계산하여np.sqrt(mse) 평가 지표 RMSE를 구함 그리고 평가 지표 R2 을 구함r2_score( )
- 선형 회귀의 Y절편 lr.intercept_과 각 피처의 회귀 계수 lr.coef_를 확인
coef = pd.Series(data = np.round(lr.coef_, 2), index = X.columns)
coef.sort_values(ascending = False)
- 회귀 모델에서 구한 회귀 계수 값lr.coef_과 피처 이름X.columns을 묶어서 Series 자료 형으로 만들고, 회귀 계수 값을 기준으로 내림차순으로 정렬하여 ascending=False 확인sort_ values( )
회귀 분석 결과를 산점도 + 선형 회귀 그래프로 시각화하기
2. 선형 회귀를 이용해 분석 모델 구축하기
import matplotlib.pyplot as plt
import seaborn as sns
fig, axs = plt.subplots(figsize = (16, 16), ncols = 3, nrows = 3)
x_features = ['AveBedrms', 'MedInc', 'HouseAge', 'Population', 'AveOccup', 'AveRooms', 'Latitude', 'Longitude']
for i, feature in enumerate(x_features):
row = int(i/3)
col = i%3
sns.regplot(x = feature, y = 'PRICE', data = boston_df, ax = axs[row][col])
- 시각화에 필요한 모듈을 임포트
- 독립 변수인 13개 피처와 종속 변수인 주택 가격, PRICE와의 회귀 관계를 보여주는 8개 그래프를 subplots()를 사용하여 3행 3열 구조로 모아서 나타냄
aborn의 regplot()은 산점도 그래프와 선형 회귀 그래프를 함께 그려줌
인공지능의 시작을 알린 퍼셉트론
▪ 이러한 상상과 함께 출발한 연구가 바로 인공 신경망(artificial neural network, 이하 줄여서 ‘신경망’이라고 함) 연구
▪ 맨 처음 시작은 ‘켜고 끄는 기능이 있는 신경’을 그물망 형태로 연결하면 사람의 뇌처럼 동작할 수 있다는 가능성을 처음으로 주장한 맥컬럭-월터 피츠(McCulloch-Walter Pitts)의 1943년 논문
▪ 그 후 1957년, 미국의 신경 생물학자 프랑크 로젠블랫(Frank Rosenblatt)이 이 개념을 실제 장치로 만들어 선보임
▪ 이것의 이름이 퍼셉트론(perceptron)


▪ 가중합(weighted sum)이란 입력 값과 가중치를 모두 곱한 후 바이어스를 더한 값을 의미
XOR 문제
▪ 이것이 퍼셉트론의 한계를 설명할 때 등장하는 XOR(exclusive OR) 문제
▪ XOR 문제는 논리 회로에 등장하는 개념
▪ 컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 ‘게이트(gate)’라고 함
▪ 그림 7-5는 AND 게이트, OR 게이트, XOR 게이트에 대한 값을 정리한 것
▪ AND게이트는 x1과 x2 둘 다 1일 때 결괏값이 1로 출력
▪ OR 게이트는 둘 중 하나라도 1이면 결괏값이 1로 출력
▪ XOR 게이트는 둘 중 하나만 1일 때 1이 출력

▪ AND와 OR 게이트는 직선을 그어 결괏값이 1인 값(검은색 점)을 구별할 수 있음
▪ XOR의 경우 선을 그어 구분할 수 없음
▪ 이는 인공지능 분야의 선구자였던 MIT의 마빈 민스키(Marvin Minsky) 교수가 1969년에 발표한 “퍼셉트론즈(Perceptrons)”라는 논문에 나오는 내용
▪ ‘뉴런 → 신경망 → 지능’이라는 도식에 따라 ‘퍼셉트론 → 인공 신경망 → 인공지능’이 가능하리라 꿈꾸었던 당시 사람들은 이것이 생각처럼 쉽지 않다는 사실을 깨닫게 됨
▪ 알고 보니 간단한 XOR 문제조차 해결할 수 없었던 것
▪ 이 논문 이후 인공지능 연구가 한동안 침체기를 겪게 됨
▪ 이 문제는 두 가지 방법이 순차적으로 개발되면서 해결
▪ 하나는 다층 퍼셉트론(multilayer perceptron), 그리고 또 하나는 오차 역전파(back propagation)
다층 퍼셉트론의 등장

다층 퍼셉트론의 설계
▪ 다층 퍼셉트론이 입력층과 출력층 사이에 숨어 있는 은닉층을 만드는 것을 그림으로 나타내면 그림 8-5와 같음

▪ 가운데 점선으로 표시된 부분이 은닉층
▪ x1과 x2는 입력 값인데, 각 값에 가중치(w)를 곱하고 바이어스(b)를 더해 은닉층으로 전송
▪ 이 값들이 모이는 은닉층의 중간 정거장을 노드(node)라고 하며, 여기서는 n1과 n2로 표시
▪ 은닉층에 취합된 값들은 활성화 함수를 통해 다음으로 보내는데, 만약 앞서 배운 시그모이드 함수(활성화 함수로 사용한다면 n1과 n2에서 계산되는 값은 각각 다음과 같음

▪ 두 식의 결괏값이 출력층의 방향으로 보내어지고, 출력층으로 전달된 값은 마찬가지로 활성화 함수를 사용해 y 예측 값을 정하게 됨
▪ 이 값을 yout이라고 할 때 이를 식으로 표현하면 다음과 같음

▪ 이제 각각의 가중치(w)와 바이어스(b) 값을 정할 차례
▪ 2차원 배열로 늘어놓으면 다음과 같이 표시할 수 있음
▪ 은닉층을 포함해 가중치 여섯 개와 바이어스 세 개가 필요함
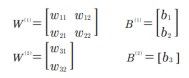
코딩으로 XOR 문제 해결하기
import numpy as np
w11 = np.array([-2, -2])
w12 = np.array([2, 2])
w2 = np.array([1, 1])
b1 = 3
b2 = -1
b3 = -1
def MLP(x, w, b):
y = np.sum(w * x) + b
if y <= 0:
return 0
else:
return 1
def NAND(x1, x2):
return MLP(np.array([x1, x2]), w11, b1)
def OR(x1, x2):
return MLP(np.array([x1, x2]), w12, b2)
def AND(x1, x2):
return MLP(np.array([x1, x2]), w2, b3)
def XOR(x1, x2):
return AND(NAND(x1, x2), OR(x1, x2))
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(x[0], x[1])
print("입력 값: " + str(x) + " 출력 값: " + str(y))'(두산로보틱스) ROKEY 부트 캠프 > Computer Vision 교육' 카테고리의 다른 글
| ep.32 딥러닝개론6 (0) | 2024.08.21 |
|---|---|
| ep.31 딥러닝개론5 (0) | 2024.08.20 |
| ep.30 딥러닝개론4 (0) | 2024.08.19 |
| ep.28 딥러닝개론2 (0) | 2024.08.14 |
| ep.27 딥러닝개론1 (0) | 2024.08.13 |





